1. 서 론
어떤 위치에서의 해수면 높이(Sea Surface Height, SSH)는 수온과 염분의 변화로 인해 밀도 구조가 달라져 발생하는 해수면 높이 편차(이후, SSHAden)와 해수의 물리적 양이 변하는 질량 가감(mass-loading)에 의한 해수면 높이 편차(이후, SSHAmass)가 변함에 따라 달라진다. 광범위한 영역의 해수면 높이를 지속적으로 측정함으로써 여러 분야의 연구에 중요한 자료를 제공하는 인공위성 고도계는 이 두 가지 효과가 다 반영된 총 해수면 높이를 측정한다.
지금까지 인공위성 고도계로 측정한 SSH와 현장 관측 자료로 산출한 역학고도(dynamic height)를 비교한 여러 연구가 수행되었다(Gilson et al. 1998; McCarthy et al. 2000; Guinehut et al. 2006). Gilson et al. (1998)과 McCarthy et al. (2000)은 각각 대만과 샌프란시스코 간, 뉴질랜드와 칠레 간 선박 이동 경로에서 5~6년 동안 XBT/XCTD로 측정한 해수 물성(수온, 염분)의 프로파일을 이용해 계산한 역학고도와 인공위성 고도계로 측정한 SSH를 비교했다. XBT 측정 한도 수심 때문에 역학고도 계산의 기준 수심이 800 m보다 얕아서, 두 해수면 높이 차이는 기준 수심보다 깊은 곳까지 이르는 소용돌이(eddy)나 해류 등의 영향 때문인 것으로 유추했고 차이를 해석하기 위해서는 깊은 수심에서의 밀도 변화에 의한 것인지 질량 가감에 의한 것인지에 대한 정보가 필요하다고 하였다. 한편 Guinehut et al. (2006)은 전지구의 XBT, XCTD, Argo 등 해수 물성 프로파일을 이용하여 기준 수심을 700 m로 한 역학고도 편차와 인공위성 고도계 SSH 편차를 비교하여 두 값이 매우 잘 일치함을 보였으며, 여러 곳에서 보이는 대규모적인 두 값의 차이는 바람에 대한 해양의 순압적 반응 때문이라고 주장하였다.
위 연구들에서 현장 관측 자료로 구한 SSH에는 SSHAmass 성분이 포함되어 있지 않다. 수온과 염분 프로파일을 이용하여 계산한 역학고도는 SSHAden에 해당하기 때문이다. 인공위성 고도계 자료의 SSH는 SSHAden 부분과 SSHAmass 부분이 전부 포함되어 있어 현장 관측 자료로 산출한 해수면 높이와 차이가 날 수 밖에 없다. 위 연구들의 인공위성 고도계 자료의 SSH와 현장 관측 자료로 산출된 SSH가 차이가 나는 원인 중 하나로 SSHAmass를 제시한 것은 이런 이유일 것으로 추측된다. 전체 SSH의 변화에서 SSHAden과 SSHAmass를 구분하는 것은 SSH 자료를 이용한 연구나 자료동화에서 중요하다(Guinehut et al. 2006). 그러나 인공위성 고도계 자료만으로는 이 둘을 구분할 수 없다. 해저면에 계류된 PIES (Pressure-recording Inverted Echo Souder)는 음파를 송신하고 송신된 음파가 해표면에 반사되어 돌아오는 데 걸린 시간, 즉 PIES와 해수면 간 음파 왕복 시간과 해저 압력을 측정한다. 이를 이용하면 SSHAden과 SSHAmass를 산출할 수 있다. PIES 측정 자료를 이용해 계산된 해수면 높이 편차(이후, SSHAPIES)와 인공위성 고도계로 측정된 해수면 높이 편차(이후, SSHASAT)를 비교한 연구들이 여러 해역을 대상으로 수행된 바 있다(Park et al. 2012; Behnisch et al. 2013; Jeon et al. 2018).
Park et al. (2012)은 쿠로시오 확장역에서 SSHAPIES의 두 성분인 SSHAden, SSHAmass와 SSHASAT의 상관관계를 조사하여 SSHAden과 SSHASAT의 상관도가 높음을 보였고 SSHAmass까지 고려하면 상관도가 더 높아진다고 하였다. Behnisch et al. (2013)은 아프리카 남쪽에서 획득한 6대의 PIES 자료를 이용하여 SSHAPIES와 SSHASAT를 비교하여 일부에서는 SSHASAT와 SSHAden의 상관계수가 SSHASAT와 SSHAden+SSHAmass의 상관계수보다 높음에 반해, 일부 정점에서는 SSHASAT와 SSHAden의 상관도가 무시할 정도임을 보였다. Jeon et al. (2018)은 북서태평양 북적도해류 영역에서 측정한 SSHAPIES가 SSHAden과 매우 유사하므로 전체 SSHA의 변동이 주로 SSHAden에 의한 것이라고 주장하였다.
PIES 자료를 이용하여 SSH 변동을 산출한 기존 연구에서 해역에 따라 SSHAPIES와 SSHASAT의 상관도에 미치는 SSHAmass의 기여도가 다름을 알 수 있다. 이는 SSH의 변동에 미치는 SSHAden과 SSHAmass의 영향이 해역에 따라 다르다는 것을 의미한다. 고위도인 Drake 해협 해역을 대상으로 한 Donohue et al. (2016)의 결과에서는 SSHAPIES의 총 분산에 SSHAmass가 기여하는 부분이 평균 19%로 매우 컸다.
팔라우 부근 해역을 대상으로 한 Andres et al. (2020)이나 북적도해류 해역에서 SSHAPIES와 SSHASAT를 비교한 Jeon et al. (2018)을 제외하면 대부분 PIES 자료를 이용하여 SSH의 변동을 조사한 연구는 고위도나 중위도를 대상으로 하였다. 본 연구에서는 필리핀과 팔라우 사이 해역에서 관측한 PIES 자료를 이용하여 SSH의 변동을 산출하였다. 그리고 SSHAPIES에서 SSHAden과 SSHAmass가 차지하는 비중을 조사하고 SSHAPIES와 SSHASAT를 비교하였다.
2. 자료 및 방법
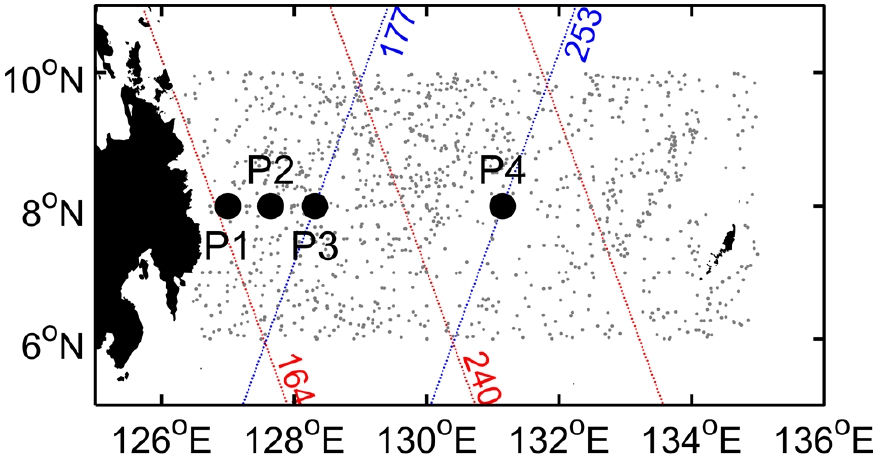
2017년 12월부터 2019년 11월까지 2년 동안 필리핀 동쪽 민다나오 해류 해역에 북위 8도를 따라 동경 127도부터 131도까지 5대의 PIES를 계류하였다. 인공위성 고도계 자료와 비교를 위해 Jason-3 인공위성 궤도 164번, 177번, 240번, 253번 상에 PIES를 계류하려 하였으나 164번 궤도에는 계류하지 못하여 필리핀에 가장 인접한 정점은 164번 궤도에서 동쪽으로 약 19 km인 곳이다. 240번 궤도 상에 계류된 PIES는 기술적인 결함으로 저장된 자료가 일주일로 자료의 길이가 충분하지 않아 나머지 4대(P1, P2, P3, P4)의 PIES 자료만을 사용하였다(Fig. 1). PIES 정점 간 거리는 각각 71 km, 73 km, 312 km이다. 앞서 기술한 바와 같이 PIES가 측정한 바닥(기기의 수심은 각각 6040 m, 5927 m, 4076 m, 4615 m)과 해수면 간 음파 왕복 시간(τ)과 바닥(해저) 압력(pbot)을 이용하면 SSHAden과 SSHAmass를 계산할 수 있다.
SSH 변화 중 밀도 변화에 의해 야기되는 성분인 SSHAden은 다음 식의 지오포텐셜 높이 편차(Φ = ϕ/g)로 계산할 수 있다.
여기서 g는 9.8 m s-2, pref는 기준 압력, 그리고 δ는 비용편차이다. 해수면과 기준 압력 사이의 δ 구조를 측정하면 Φ를 계산할 수 있지만 측정하지 못하더라도 τ를 측정함으로써 Φ를 추정할 수 있다. Φ의 평균을 제거한 값(Φa)이 SSHAden에 해당하고 이를 ηbc로 표시하였다. 한편, SSH 변화 중 질량 가감에 의해 야기되는 성분인 SSHAmass는 pˊbot/ρbg로 계산할 수 있고 이를 ηref로 표시하였다. 여기서 pˊbot는 바닥 압력 편차이며 ρb는 해저 밀도로 1037 kg m-3이다. 그리고 총 SSHA는 ηbc와 ηref의 합으로 ηtot (= ηbc + ηref)로 표시하였다.
τ는 음파가 왕복하는 바닥과 해수면 간 거리와 음파가 통과하는 해수의 밀도 구조에 의해 달라진다. τ를 이용하여 Φ를 추정하려면 τ에 영향을 주는 성분 중 밀도 구조와 연관된 부분만 계산하여야 한다. 즉, 해수면이 오르내려서 바닥과 해수면 간 거리가 변하는 부분을 제거하여야 한다. 해수의 질량 가감에 의한 해수면 이동은 pbot를 이용해 계산할 수 있고 기압에 의한 해수면 승강, 즉 역기압 반응은 표층 대기압(patm)을 이용해 계산할 수 있다. 따라서 측정된 τ에서 질량 가감과 역기압 반응에 의한 해수면 승강으로 야기된 부분을 보정한 후 Φ 추정에 이용하였다. 역기압 반응 계산에는 공간 해상도가 0.25° × 0.25°이고 시간 해상도는 6시간인 European Center for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA5)의 patm 자료를 사용하였다(Hersbach et al. 2020). τ로 Φ를 추정하기 위해서는 해수 물성 프로파일이 필요하여 영국 기상청 Hadley 센터의 EN4 자료(Good et al. 2013) 중 북위 6~10도, 동경 125.5~135도 영역의 수온과 염분 프로파일을 이용하였다(Fig. 1의 회색 점).
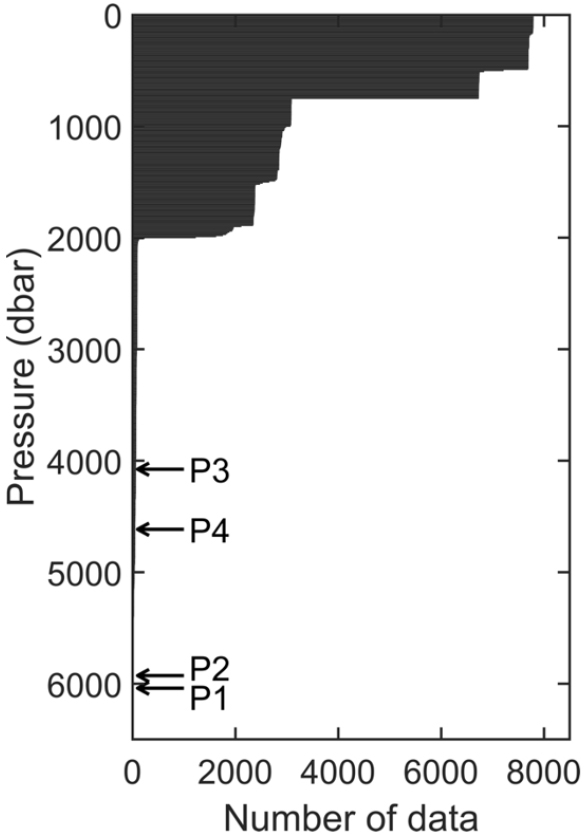
바닥에 설치된 PIES로 측정한 τ로 Φ를 추정하려면 τ에 영향을 주는 수심 범위 전체에서 해수 물성 프로파일이 필요하다. 즉, 해수면부터 바닥까지 δ의 연직 구조를 알아야 Φ (Φbot)를 계산할 수 있고 해수면과 바닥 간 τ (τbot)와 Φbot의 관계를 구할 수 있다. 그러나 기기가 설치된 수심이 깊어 EN4 자료 중 해당 수심까지 관측된 프로파일의 수는 매우 적다(Fig. 2). 따라서 더 많은 프로파일을 사용하여 τ와 Φ의 관계의 신뢰성을 높이기 위해 기준 수심을 바닥 수심 대신 2000 dbar로 정하였다.
2000 dbar보다 깊은 수심의 밀도 변화는 해수면부터 2000 dbar까지 밀도 변화에 비해 상대적으로 매우 작으므로 ηbc 변동을 Φbot 변동 대신 Φ2000 변동으로 나타낼 수 있다. 따라서 τbot을 τ2000으로 변환하고 τ2000과 Φ2000의 관계를 구할 수 있으면 PIES로 측정된 τbot 변동을 Φ2000 변동, 즉 ηbc 변동으로 변환할 수 있다.
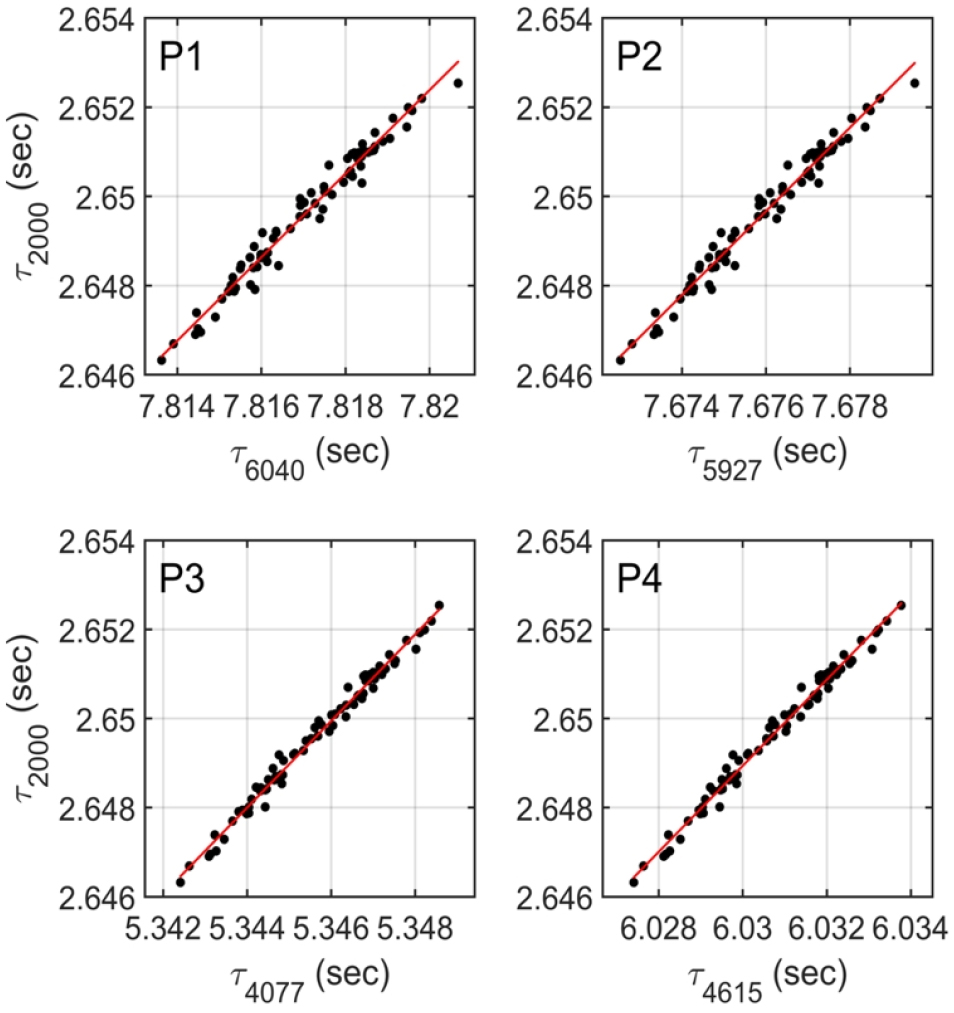
각 정점의 τbot을 τ2000로 변환하기 위해 4000 dbar보다 깊게 관측된 77개의 프로파일을 사용하여 2000 dbar와 각 정점의 바닥 간 τ를 추정하였다. 4000 dbar보다 깊은 곳의 연직 물성 변화는 무시할 만큼 작아서 프로파일의 최대 관측 수심부터 6040 dbar까지 물성은 최대 관측 수심의 물성과 같도록 외삽하였다. 외삽된 프로파일로 구한 각 정점의 τbot과 τ2000의 관계는 Fig. 3과 같다. 각 정점에서 τbot과 τ2000의 일차 관계가 뚜렷하고 root-mean-square (rms) 오차가 작으므로(0.0002초, 0.2 ms) 각 정점의 τbot을 τ2000로 변환하는 데 무리가 없다.
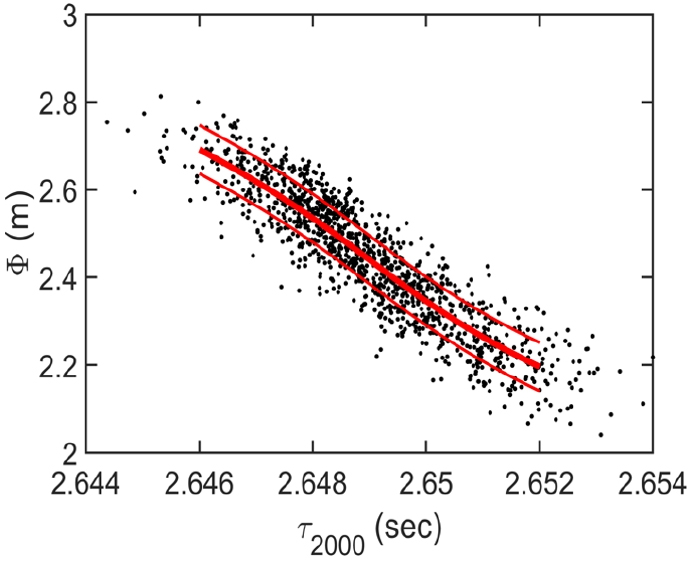
기준 수심인 2000 dbar보다 깊게 관측된 1231개의 프로파일을 이용하여 τ2000과 Φ의 관계를 구하였다(Fig. 4). τ2000에서 ηbc로 변환의 rms 오차는 5.5 cm이다. τ2000에서 Φ로 변환의 기울기는 약 8.3 cm/ms이므로 τbot에서 τ2000로 변환의 rms 오차인 0.2 ms는 약 4.2 cm의 rms 오차를 유발할 수 있다. 관측 자료에는 대기압이나 조석, 해양 상태 등에 의해 오차가 포함되어 있는데(Baker-Yeboah et al. 2009) 이 오차는 약 1 cm 정도이다. 따라서 τbot로 ηbc를 산출하는 데 생기는 총 rms 오차는 약 6.9 cm ()이다.
인공위성 고도계 자료는 공간 해상도가 1/4도이고 시간 간격은 1일인 AVISO 격자 자료를 사용하였다(AVISO 2020). AVISO는 단주기 바람과 기압의 외력에 의해 야기되는 단주기 해수면 반응을 제거하기 위해 동적 대기 보정(Dynamic Atmospheric Correction, DAC)을 적용한다. 따라서 SSHAPIES와 SSHASAT의 비교에 동일 조건을 적용하기 위해 ηref 계산에도 DAC를 적용하였다. DAC와 patm을 추가하여 20일 미만 주기의 DAC 유도 압력을 계산하고(Park et al. 2012) ηref를 구하기 전에 pˊbot에서 DAC 유도 압력 성분을 제거하였다.
3. 결 과
SSHAPIES
2년 동안 관측된 PIES 자료로 산출한 ηbc, ηref와 ηtot의 변동을 조사하였고, ηtot 분산에 대한 ηbc와 ηref의 상대적 기여도를 σ2 = σ2bc + σ2ref + 2cov(ηbc, ηref)로 계산하여 Table 1에 제시하였다. ηtot 분산은 P2에서 가장 크고 P1에서 가장 작다. ηtot 분산이 P2, P3에서 크고 P1, P4에서 작은 양상이 보이는데, ηbc 분산도 이와 유사한 양상을 보임에 비해 ηref 분산은 외해쪽 정점인 P3, P4에서 더 큰 양상을 보인다. ηbc가 ηtot 분산에 기여하는 정도는 P1에서 98%이고 P3에서 최대인 103%로 외해로 갈수록 커지는 양상이나 가장 외해쪽에 위치한 P4에서는 ηbc의 기여도가 88%로 다른 정점들에 비해 작은 특징을 보인다. ηref가 ηtot 분산에 기여하는 정도는 3% 미만으로 작고 특히 ηbc 분산이 가장 큰 P2에서 최소이다.
Table 1.
Variance (cm2) of ηbc, ηref, and ηtot and percent variance (%) captured by ηbc and ηref
| Site | σ2bc | σ2ref | σ2 | σ2bc/σ2 | σ2ref/σ2 |
| P1 | 117.9 | 3.2 | 120.6 | 97.7 | 2.6 |
| P2 | 197.0 | 3.0 | 195.8 | 100.5 | 1.5 |
| P3 | 173.3 | 3.4 | 167.9 | 103.2 | 2.0 |
| P4 | 119.4 | 3.8 | 134.9 | 88.5 | 2.8 |
Φ 계산에 사용되는 pref의 선택에 따라 ηtot에서 ηbc가 차지하는 기여도가 달라질 수 있는데 그 정도는 성층의 강도에 따라 달라 성층이 약한 지역에서 특히 영향이 크다. 인공위성 고도계 자료와 Argo 자료를 이용하여 SSHASAT와 역학고도 편차(Dynamic Height Anomaly, DHA; SSHAden에 해당)를 비교한 Dhomps et al. (2011)은 DHA 계산에 사용하는 기준수심(pref에 해당)으로 적도 해역에서는 300~ 400 m 정도면 충분하다고 제시하였다. pref = 400 dbar로 하여 동일한 방법으로 구한 ηbc를 pref =2000 dbar인 경우의 ηbc와 비교하면 차이가 미미하여(rms 오차 2 cm 이하), pref = 2000 dbar로 하거나 400 dbar로 하거나 ηtot는 크게 다르지 않다. 따라서 ηtot 분산에 기여하는 ηbc의 몫은 pref 선택과 무관함을 알 수 있다. 한편 Φ 계산에 4배 이상 많은 프로파일을 사용한 pref = 400 dbar인 경우의 ηtot가 pref = 2000 dbar인 경우의 ηtot와 매우 유사함은 본 연구에서 Φ 계산에 사용한 프로파일의 수는 충분함을 시사한다.
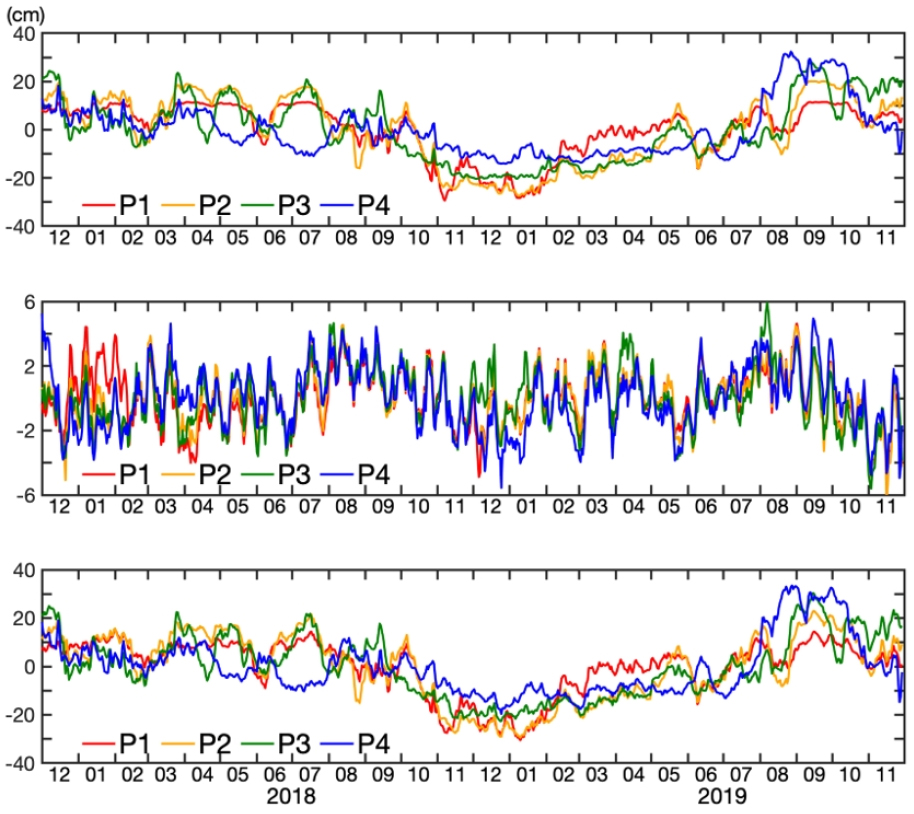
2년간 ηbc 변화폭은 40 cm 정도로 10 cm 정도인 ηref 변화폭의 약 4배 정도 되며, ηref가 한 달에 두 번의 변동이 두드러지게 나타남에 비해 ηbc는 한 달보다 긴 주기의 변동이 뚜렷하다(Fig. 5). 정점들의 ηbc 간 상관계수는 정점 간 거리가 가까울수록 큰 경향이 있다(Table 2). P1, P2, P3의 ηbc 간 상관계수는 0.76 이상임에 비해 P4의 ηbc와 다른 세 정점의 ηbc의 상관계수는 0.62 이하로 95% 신뢰수준(자기상관도로 구한 자유도를 이용) 아래이다(Table 2). 전체적으로 ηbc는 2018년 11월~2019년 1월 경에 가장 낮고 2019년 8~10월 경에 가장 높은 양상을 띤다. P4의 ηbc 변동은 다른 정점의 ηbc 변동과 다른 양상이 보이는데 특히 2018년 4월 중순~7월 하순에 P4의 ηbc가 다른 정점의 ηbc와 반대로 변동하는 양상이 특이하다.
Table 2.
Correlation coefficients between SSHAs of the observation sites. Values in bold font indicate those above 95% confidence level
정점 간 ηref의 상관계수는 0.67 이상으로 전체적으로는 대부분의 시기에 네 정점의 ηref가 매우 유사하다. 그러나 시기에 따라 어떤 정점의 ηref가 다른 정점들의 ηref와 차이가 큰 경우도 종종 보인다. P1의 ηref는 인접한 P2의 ηref와 상관계수가 0.9 정도로 유사한 변동성을 보이지만 2018년 1월 중순~2월 상순에 특이하게 높다. 가장 외해에 있는 P4의 ηref는 2017년 12월 상순에는 다른 정점의 ηref보다 높지만, 2018년 12월 하순~2019년 1월 중순 기간에는 낮은 양상이 보인다. 한편, P3의 ηref가 서쪽의 P2나 동쪽의 P4의 ηref와 다른 변동을 보이는 기간이 있다. 2018년 12월 초중순과 2019년 4월 상순에 P2와 P4의 ηref는 유사한데 중간에 위치한 P3의 ηref가 이들보다 높은 점은 특이하다. 이런 특징 때문에 P2와 P4의 ηref 간 상관계수가 P3와 P4의 ηref 간 상관계수보다 높게 나오는 것으로 판단된다.
모든 정점에서 ηbc와 ηtot는 매우 유사하며(Fig. 6, 상관계수 0.99), 이는 이 해역의 SSHA 변동이 주로 SSHAden에 의해 좌우됨을 의미한다. 본 연구 해역의 동쪽인 팔라우 인근에서 획득한 CPIES 자료를 조사한 Andres et al. (2020)도 SSHA의 중규모 변동성이 주로 SSHAden의 변동성에 기인한다고 하였으며 ηbc와 ηtot 시계열이 매우 유사하다고 하였다. 각 정점에서 ηtot와 ηbc의 상관계수가 매우 높기 때문에 정점 간 ηtot의 상관계수도 정점 간 ηbc의 상관계수와 매우 유사하여 정점 간 거리가 가까울수록 큰 경향이 있다.
SSHASAT와 SSHAPIES 비교
AVISO에서 제공하는 지연 모드 격자 자료를 이용하여 SSHASAT과 SSHAPIES를 비교하였다. 정점 간 SSHASAT의 상관계수는 SSHAPIES의 그것보다 크다(Table 2). 정점 간 ηtot의 상관계수가 정점 간 거리가 가까울수록 큰 경향이 있는 것처럼 정점 간 SSHASAT의 상관계수도 정점 간 거리가 가까울수록 크지만 P1–P2의 ηtot 간 상관계수가 P2–P3의 ηtot 간 상관계수보다 큰 것과 달리 P1–P2와 P2–P3의 SSHASAT 간 상관계수는 거의 같다.
각 정점의 SSHASAT 분산은 52~117 cm2의 범위로 123~ 198 cm2인 ηtot 분산보다 작다. SSHASAT 분산은 P4 > P3 > P2 > P1으로 P2 > P3 > P4 > P1인 ηtot 분산과 분포가 다르며 SSHASAT 분산과 ηtot 분산의 차이는 P2에서 가장 크고 P4에서 가장 작다.
ηtot와 SSHASAT의 상관계수는 P3 > P2 > P4 > P1이며 ηbc와 SSHASAT의 상관계수도 순서가 동일하지만 ηtot와 SSHASAT의 상관계수가 ηbc와 SSHASAT의 상관계수보다 작은 점이 특이하다(Table 3). 이런 경향은 각각 쿠로시오 확장역과 북적도해류역에서 SSHAPIES와 SSHASAT의 상관관계를 조사한 Park et al. (2012)과 Jeon et al. (2018)의 결과와 다르다. 즉, 두 연구에서는 ηbc와 SSHASAT의 상관도보다 ηref까지 고려된 ηtot와 SSHASAT의 상관도가 큰데 본 연구 해역에서는 ηbc와 SSHASAT의 상관도보다 ηtot와 SSHASAT의 상관도가 작다.
Table 3.
Comparisons between SSHASAT and SSHAPIES. Values are expressed as ηtot (ηbc). cr and rms denote correlation coefficient and rms difference, respectively
| P1 | P2 | P3 | P4 | |
| cr | 0.79 (0.81) | 0.83 (0.84) | 0.85 (0.85) | 0.83 (0.83) |
| rms | 6.93 (6.52) | 8.28 (8.19) | 6.99 (7.04) | 6.66 (6.32) |
ηtot의 분산에 ηref가 기여하는 정도가 큰 고위도 지역에서는 ηtot와 SSHASAT의 상관도보다 ηbc와 SSHASAT의 상관도가 큰 경우가 있으나 이 경우 ηref와 SSHASAT의 상관도도 무시할 정도가 아닌데(Behnisch et al. 2013), ηref와 SSHASAT의 상관도가 거의 없는 본 연구 해역에서 ηtot와 SSHASAT의 상관도보다 ηbc와 SSHASAT의 상관도가 큰 점은 주목할 만하다. 일반적으로 SSHASAT는 ηref가 포함되지 않은 ηbc보다 모든 성분을 포함한 ηtot와 더 유사성이 높을 것으로 추측된다. 본 연구 해역에서 ηtot와 SSHASAT의 상관도보다 ηbc와 SSHASAT의 상관도가 큰 점과 ηref와 SSHASAT의 상관도가 거의 없다는 점은 인공위성 고도계 자료의 보정 과정 중 이 해역의 순압성 신호에 대한 보정에 오차가 있을 가능성을 시사한다고 판단된다.
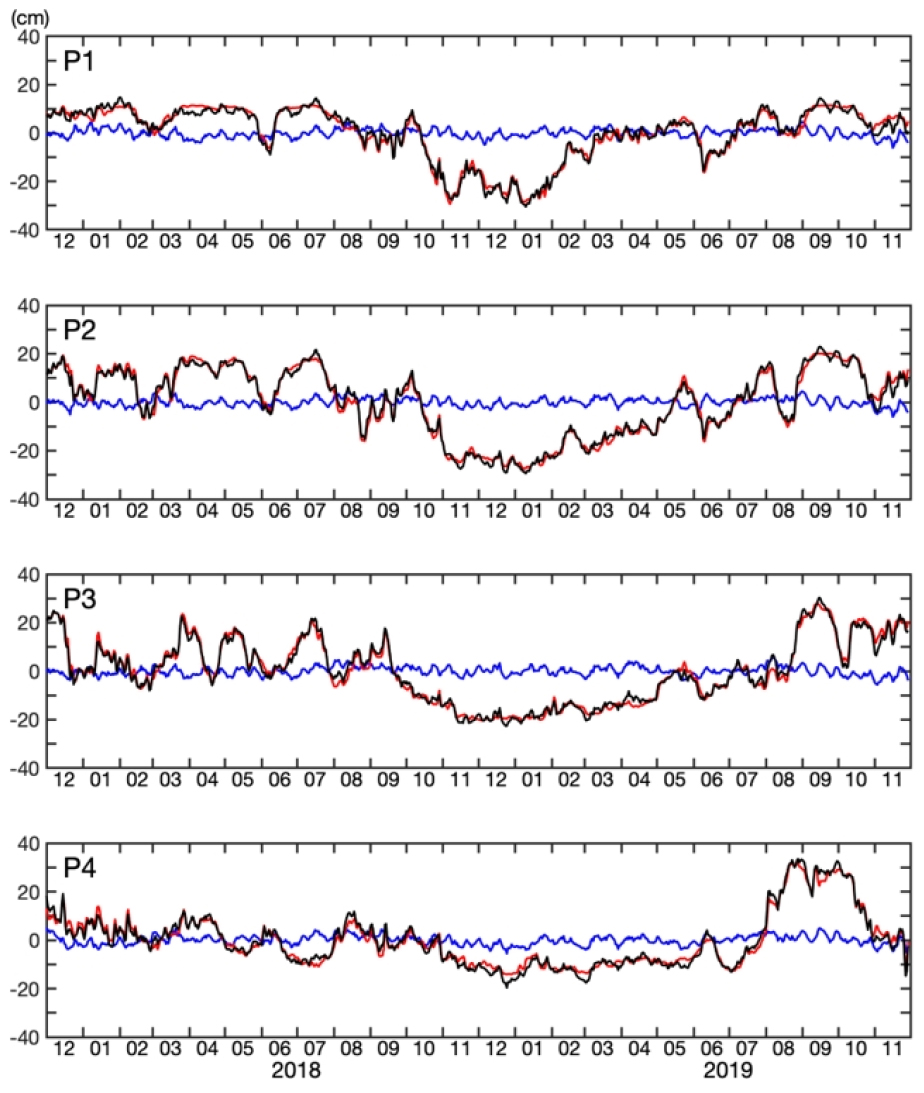
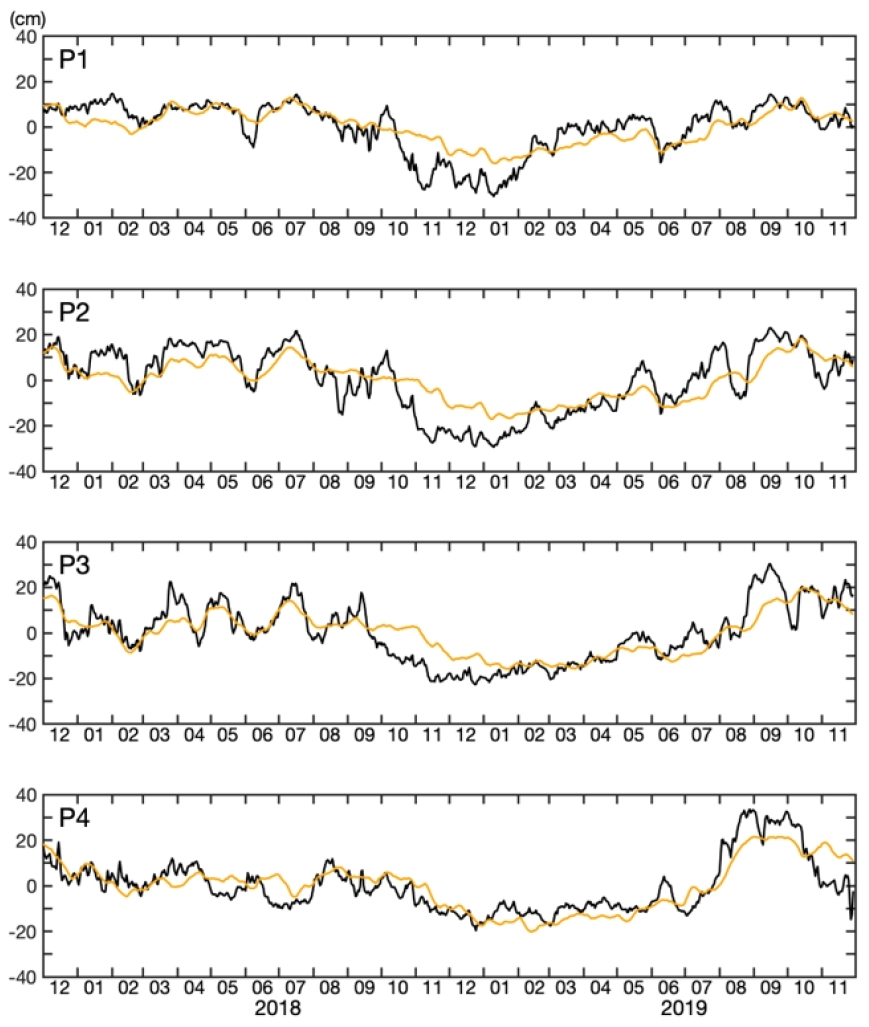
ηtot와 SSHASAT의 rms 차이는 P2 > P3 > P1 > P4이며 ηbc와 SSHASAT의 rms 차이도 순서가 동일하다. P3를 제외하면 ηtot와 SSHASAT의 rms 차이가 ηbc와 SSHASAT의 rms 차이보다 크다. 이 역시 ηref까지 고려된 ηtot와 SSHASAT의 rms 차이가 ηbc와 SSHASAT의 rms 차이보다 작다는 Park et al. (2012)의 결과와 다르다. Park et al. (2012)의 결과처럼 상관계수가 클수록 rms 차이가 작은 경향이 일반적인데 본 연구 해역에서는 각 정점의 ηtot와 SSHASAT의 상관계수와 rms 차이의 크기 순서가 반대가 아닌 점이 특이하다. 특히 P2의 rms 차이가 다른 세 정점에서의 rms 차이보다 큰데 이는 P2에서 큰 ηtot (또는 ηbc)의 한달 이내의 급격한 상승이나 하강의 변동이 SSHASAT에서는 보이지 않기 때문인 것으로 판단된다(Fig. 7).
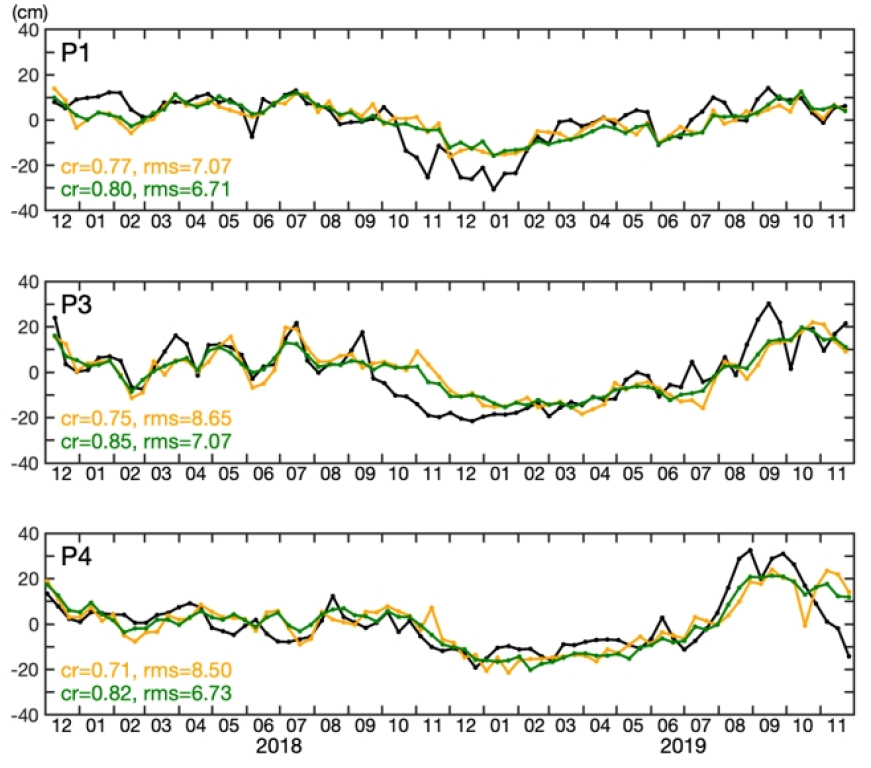
SSHASAT와 ηtot의 차이가 여러 고도계 자료를 종합하는 과정이나 격자화하는 과정에서 오류가 발생하여 생기는 것인지는 단일 고도계 자료를 조사함으로써 확인할 수 있다. P1의 SSHAPIES는 19 km 떨어진 Jason-3 164번 궤도의 자료와, P3와 P4의 ηtot는 177번 궤도와 253번 궤도의 자료와 비교하였다(AVISO 2018). 단일 고도계 자료의 SSHA (이후, SSHAMONO)는 9.92일 간격으로, 일관된 비교를 위해 ηtot와 SSHASAT도 SSHAMONO의 시기에 해당하는 값을 사용하였다(Fig. 8). ηtot와 SSHAMONO의 상관계수는 ηtot와 SSHASAT의 상관계수보다 작고 rms 오차는 크다. 이는 SSHASAT가 SSHAMONO보다 더 ηtot와 유사하다는 것을 의미한다. SSHASAT가 SSHAMONO보다 ηtot와 더 유사한 현상은 Jeon et al. (2018)이 북적도해류역의 자료로 보인 바 있고 그 이유로 SSHASAT가 SSHAMONO에서 보이는 hump 오차를 완화시킨 점을 든 바 있다. 따라서 본 연구 해역에서 보이는 SSHASAT와 ηtot의 차이가 여러 고도계 자료를 종합하는 과정이나 격자화 과정에서 오류가 발생하여 SSHASAT에 오차가 포함되었기 때문이 아님을 알 수 있다.
P1의 ηtot는 SSHASAT보다 2018년 1월~2월, 2019년 3~9월에 높고 2018년 11월~2019년 1월에 낮다(Fig. 7). P2에서는 전체적으로 P1과 비슷하지만 2018년 1월~2월뿐만 아니라 2018년 3월~5월에도 ηtot가 SSHASAT보다 더 높은 형태를 보이며 2019년 3월~4월에는 ηtot가 SSHASAT보다 낮은 형태를 보인다. P1과 P2에서는 ηtot의 급격한 하강이 2018년 10월에 나타나 10월 중순부터 SSHASAT보다 낮아지는데 P3에서는 ηtot가 2018년 9월 중순부터 낮아지는 점이 약간 다르다. P3에서는 ηtot가 SSHASAT보다 가장 높은 시기는 2019년 9월이다. P1~P3에서 ηtot와 SSHASAT의 차이가 두드러진 시기는 2018년 10월~1월로 ηtot가 SSHASAT에 비해 현저하게 낮은데 P4에서는 이런 특징이 나타나지 않는다. P4에서는 2019년 8월~11월의 시기를 제외하면 ηtot와 SSHASAT가 크게 차이 나지 않는데 이러한 점 때문에 rms 차이가 P4에서 최소인 것으로 판단된다. 2019년 10월~11월에 SSHASAT 변동은 크지 않은데 ηtot는 급격하게 낮아지는 모습이 두 SSHA의 두드러진 차이이다.
4. 요약 및 고찰
2017년 12월부터 2019년 11월까지 약 2년간 필리핀 동쪽 민다나오 해류 해역의 북위 8도선 상에 계류된 4대의 PIES 자료를 이용하여 밀도 변화에 의한 SSHA와 질량 가감에 의한 SSHA를 계산하고 인공위성으로 측정된 SSHA와 비교하였다. 2년 간 ηbc의 변화폭은 40 cm 정도로 한 달보다 긴 주기의 변동이 뚜렷함에 비해 ηref는 한 달에 두 번의 변동이 두드러지고 변화폭은 10 cm 정도이다. 모든 정점에서 ηbc와 ηtot는 매우 유사하여 이 해역의 SSHA 변동이 주로 밀도 변화에 의한 것으로 판단된다. ηtot와 ηbc의 분산은 P2, P3에서 크고 P1, P4에서 작음에 비해 ηref 분산은 외해쪽 정점인 P3, P4에서 더 크다. ηref가 ηtot 분산에 기여하는 정도는 3% 미만으로 작다. ηbc 간 상관도는 정점 간 거리가 가까울수록 큰 경향이 있으나 P4의 ηbc는 다른 세 정점의 ηbc와 상관도가 낮다.
Na et al. (2012)는 쿠로시오 확장역 해역에서 획득된 바닥 압력 자료에서 보이는 13일 부근의 강한 변동성이 북태평양의 넓은 지역에 걸친 큰 규모의 바람 응력 컬(curl)에 의해 유도되며 해저 지형이 이러한 변동성의 전파와 출현 범위에 영향을 미친다고 주장하였다. 본 연구 해역에서 보이는 ηref 변동성도 큰 규모의 바람장과 해저 지형과 연관되었을 것으로 추측된다. 한편, Andres et al. (2020)은 팔라우 인근에서 보이는 20~200일 주기대의 밀도약층(pycnocline) 변동성을 중규모 소용돌이가 서쪽으로 전파하는 현상에 의한 것으로 설명하였다. 팔라우 서쪽에 위치한 본 연구 해역에서 보이는 한 달보다 긴 주기의 ηbc 변동도 이러한 중규모 소용돌이의 서향 전파에 의한 것으로 판단된다.
SSHASAT 분산은 ηtot 분산보다 작으며 둘의 차이는 P2에서 가장 크고 P4에서 가장 작다. SSHASAT와 ηtot의 상관계수는 P2, P3, P4에서 0.83~0.85로 비슷하고 P1에서 가장 작으며, rms 차이는 P4에서 가장 작고 P2에서 가장 크다. SSHASAT와 ηtot의 상관계수는 SSHASAT와 ηbc의 상관계수보다 작아 이 해역에서는 오히려 ηref가 포함되면 SSHAPIES와 SSHASAT의 상관도가 작아진다.
Guinehut et al. (2006)나 Dhomps et al. (2011)은 SSHASAT와 DHA가 매우 잘 일치한다고 하였고, 본 연구의 대상 해역은 다른 해역에 비해 상관도가 높은 해역에 속한다(Guinehut et al. (2006)의 Fig. 1 참조). Guinehut et al. (2006)은 SSHASAT와 DHA의 차이를 바람에 대한 해양의 순압적 반응과 연관 지었다. 즉, SSHASAT – DHA를 SSHAmass로 추정하여 Sverdrup 수송과 비교하였다. 이러한 추정은 SSHASAT이 ηtot와 같은 경우, 즉 ηref = SSHASAT - ηbc라는 추정인데 본 연구에서 SSHASAT - ηbc의 분산이 ηref 분산의 10배가 넘을 정도로 둘 사이의 차이는 커서 이러한 추정을 뒷받침하는 결과가 나오지 않았다. SSHASAT와 ηtot의 차이가 SSHASAT에 포함된 이 해역의 순압성 신호에 대한 보정 오차에 기인한 것인지 τ에서 Φ로의 변환 과정의 오차에 기인한 것인지를 밝히기 위해서는 더 면밀한 조사가 요구된다.