1. 서 론

주로 바람에 의해 야기되는 해양 표층 준관성진동(near-inertial oscillation)은 코리올리 효과가 없는 적도를 제외하면 전 세계 해양 어디나 존재할 수 있다. 바람에 의해 발생된 준관성진동은 혼합층 기저면에 수직전단(vertical shear)을 유도하여 혼합층 두께를 변화시킬 수 있으며(Jochum et al. 2013), 일부의 에너지는 혼합층 밑으로 전달되어 해양내부의 연직혼합을 야기할 수 있다(Alford et al. 2016; Garrett 2001; Munk and Wunsch 1998; Jiang et al. 2005; Nycander 2005).

동해의 준관성진동은 겨울 몬순이나 태풍과 같은 강한 바람에 의해 주로 발생한다고 알려진다(Jeon et al. 2019; Song et al. 2020; Kawaguchi et al. 2023). 작은 대양이라 불리는 동해는 중규모 소용돌이가 활발한 해역으로 해양 배경장이 준관성진동 에너지의 재분배에 영향을 미치기도 한다(Park and Watts 2005; Byun et al. 2010; Jeon et al. 2019; Song et al. 2020; Kawaguchi et al. 2020; Noh and Nam 2021). 동해의 준관성진동에 대한 다양한 기존 연구는 공간적으로 한정된 계류관측, 단기간의 간헐적 라그랑지안 관측, 시간적 및 공간적 고해상도 수치모형을 활용한 결과로, 다년간의 실측자료에 근거한 동해 전체를 아우르는 준관성진동 특성에 대한 확인과 고찰이 부족하다. Park et al. (2004)는 1999–2003년 아르고(Argo)의 표층 표류 궤적과 표층뜰개를 활용하여 동해 준관성진동 크기에 대한 통계량을 분석하고, 추가 자료의 축적을 통해 보다 상세한 연구가 가능할 것이라는 가능성을 제시한 바 있다. 그러나 아르고의 표층 체류시간의 단축으로, 장기간의 자료가 충분히 축적되지 않아 상세한 분석을 진행하기에는 한계가 있다.

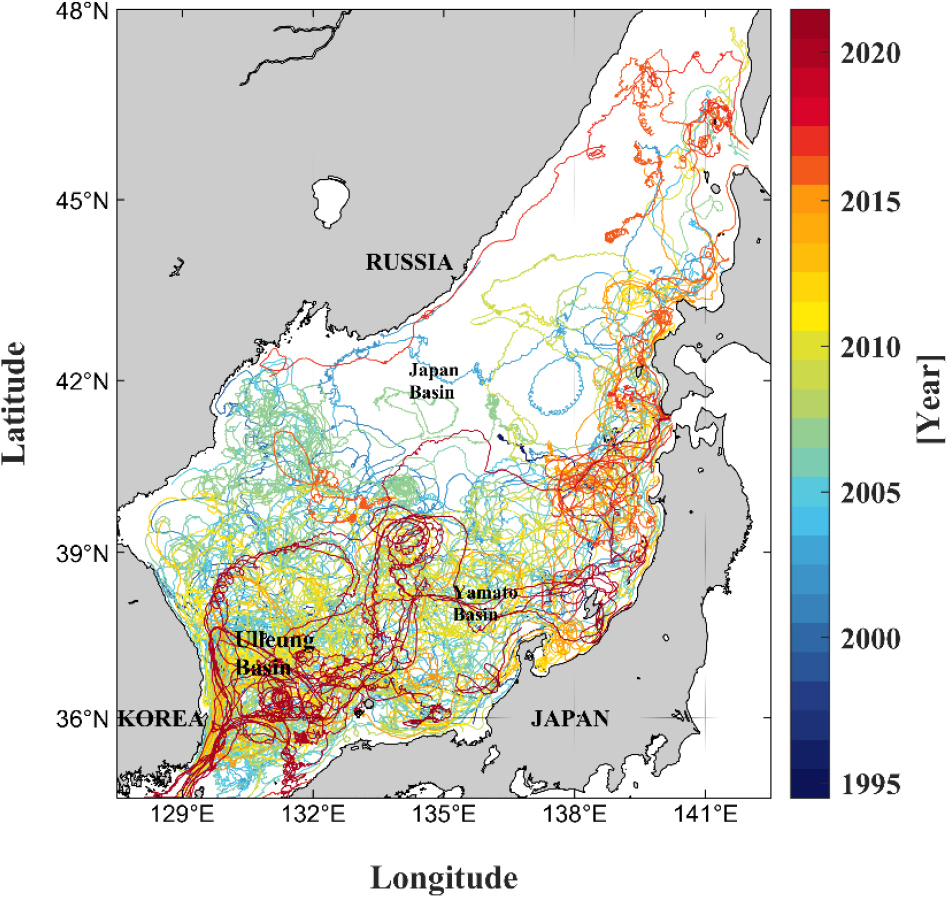
표층뜰개는 2005년 1월 이후에 위치추적 위성이 2개에서 5개로 늘어나면서 뜰개 위치 정확도가 크게 향상되었고, 최근 Global Drifter Program (GDP)에서는 기존의 6시간 이하 간격 자료만을 재처리하여 1시간 간격 자료를 제공한다(Elipot and Lumpkin 2008; Elipot et al. 2010). 재처리된 1시간 간격의 전 세계 해양 GDP 표층뜰개 자료는 반일주기 및 일주기 조석과 관성주기 해양현상이 잘 나타나고 있으며(Elipot et al. 2010; 2016), 20년 이상의 장기 자료가 축적되었다. 본 연구에서는 동해 전역에 준하는 영역에서 총 27년간의 GDP 표층뜰개 관측자료를 분석하여(Fig. 1) 준관성진동의 시간적 및 공간적 특성을 확인하고 기존 연구결과와 비교 및 재고찰하였다.

Fig. 1.

Trajectories of GDP surface drifters from 1995–2021 in the East Sea

2. 자료 및 방법

자료

미국 국립해양대기관리청(National Oceanic and Atmospheric Administration, U.S. Department of Commerce, NOAA)에서 제공하는 1시간 간격 동해 표층뜰개(Global Drifter Program, GDP) 자료를 사용하였다(https://www.aoml.noaa.gov/phod/gdp/hourly_data.php). GDP자료는 고유 식별 번호, 수온, 위치, 동서 및 남북 방향 유속, 드로그(drogue) 유실 날짜 등의 정보가 함께 제공된다. 표층부표 밑 약 15 m에 중심이 위치되도록 설치된 드로그(drogue)는 표층뜰개가 바람 영향을 줄이고 해류 영향을 크게 받게 하며, 드로그가 유실될 경우 바람 효과의 영향이 커지게 된다(Laurindo et al. 2017). 이에 본 연구에서는 드로그가 부착된 1995년부터 2021년(27년)의 표층뜰개 자료만을 활용하여 준관성진동 분석을 수행하였다.

바람과 준관성진동의 관계를 살펴보기 위하여 유럽 중기기상예보센터(European Center for Medium Range Weather Forecasts, ECMWF) ERA5 재분석장의 0.25°× 0.25° 공간해상도의 1시간 간격 바람자료를 사용하였다. 혼합층 두께와 준관성진동 관계를 함께 살펴보고자 표층 밀도로부터 0.03 kg m^-3 밀도차가 나타나는 수심으로 계산된 ECMWF의 Ocean Reanalysis System 5(ORAS5) 월 평균 혼합층 두께 자료를 사용하였으며, 0.25° × 0.25°의 공간해상도를 갖는다. ORAS5 자료는 해수면 온도, 염분, 평균 해수면 추세를 반영한다. 2014년 이전 자료는 재분석된 대기 강제력과 재가공된 관측치를 활용하여 계산되며, 2015년 이후 자료는 준실시간 대기 강제력과 관측치를 활용하여 산출된다. 위성 고도계로 산출된 일별 지형류는 Copernicus Marine Environment Monitoring Service에서 제공하는 4단계 격자 데이터를 활용하여 상대와도(ζ=∂v∂x-∂u∂y)를 계산하였으며, 공간해상도는 0.25° × 0.25°이다.

준관성진동의 계절적 특성에 미치는 태풍의 영향을 확인하기 위하여 미국 국립해양대기관리청 국립환경정보센터(National Centers for Environmental Information)의 International Best Track Archive for Climate Stewardship (IBTrACS)의 3시간 간격 태풍 위치 자료를 사용하였다.

방법

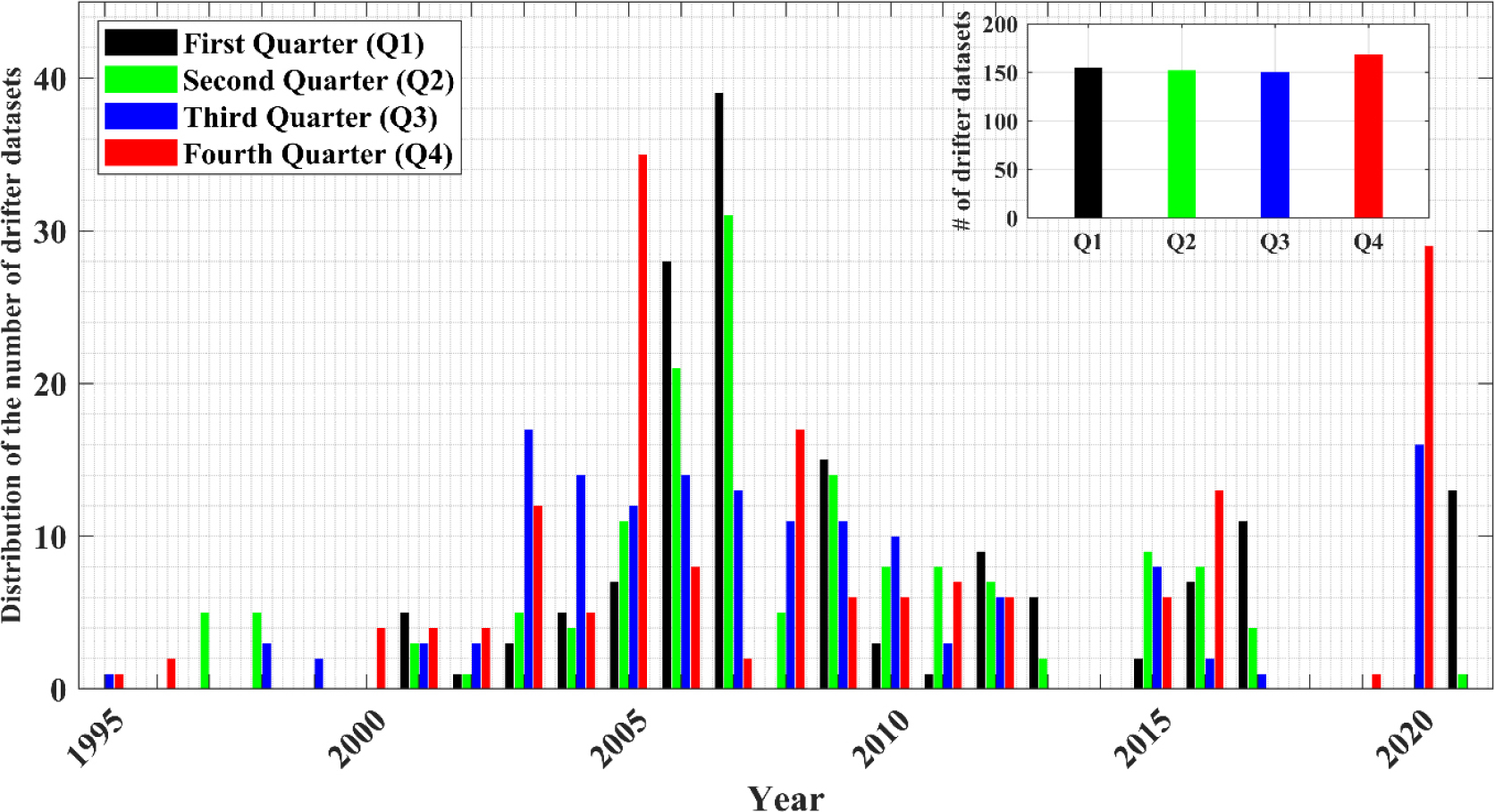
표층뜰개 궤적에 12시간 이상의 연속된 공백이 존재할 경우, 서로 다른 자료로 분리하여 구성하였으며, 그 외의 경우는 선형 보간을 하였다. 보간 및 재구성한 시계열자료의 길이가 170시간(약 7일)이하인 자료는 사용하지 않았고, 구분된 시계열자료는 총 347세트였다. 구분된 표층뜰개 시계열 자료 세트 중 여러 월에 자료가 걸치는 경우는 해당 월의 시계열이 170시간 이상일 때만 그 월에 유효한 표층뜰개 자료가 존재하였다고 간주하였다. 예를 들어 1개의 표층 뜰개가 6월 24일부터 7월 7일까지 표류하였다면 6월(자료 길이 7일)과 7월(자료 길이 7일)의 자료 세트는 각각 1세트, 6월 25일부터 7월 7일까지 표류한다면 6월(자료 길이 6일)은 자료가 없고 7월(자료 길이 7일)에만 1세트가 존재하게 된다. 분기별 뜰개는 각 분기에 해당하는 월의 표층뜰개 자료세트를 합산하여 계산하였다(Fig. 2). 각 분기별로 살펴보면 모든 분기에서 약 150세트 내외로 고르게 분포하였으며(Fig. 2), 월별 계산에 활용된 표층뜰개 또한 40세트 내외로 비슷하였다(Fig. 7b).

Fig. 2.

Distribution of the number of drifter datasets in each year and quarter (Q1: January–March, Q2: April–June, Q3: July–September, Q4: October–December). The upper-right panel indicates the sum of drifter datasets for each quarter

동해 위도 34.5–48°N 해역의 관성 주기는 약 16–21.2시간이며, Butterworth filter를 적용하기 위해서는 오일러리안 관측과 같이 동일한 위치에서의 충분한 길이의 시계열 자료가 필요하다. 그러나 표층뜰개와 같은 라그랑지안 관측은 시공간적 위치 변화로 준관성진동의 주기가 다소 변형되어 관측될 수 있다. Son et al. (2022)과 Halle and Pinkel (2003)에서 제시된 방법으로 준관성진동의 주파수(effective inertial frequency)를 계산한 결과(상대와도는 기존 연구들(Park et al. 2005; Jeon et al. 2019)에서 최댓값으로 보이는 2×10-5(s-1)을 사용), 위도 36–42°N (표층뜰개가 가장 많이 분포한 해역)에서는 약 16.2–23.3시간으로 산출되며, 이는 local inertial frequency에 비하여 약 10% 차이가 있고 최대 ~15%까지 차이를 보인다. 본 연구에서는 4차 Butterworth 대역 통과 필터(4th-order Butterworth band-pass filter)를 사용하고, 편의상 모든 표층뜰개를 동일한 15–23시간 주기의 밴드폭으로 필터링하여 준관성진동을 추출하였다. 본 방법은 23시간을 초과하는 주기를 완전히 포함할 수 없으므로 동해 남부에서 상대와도가 매우 강한 위치에서는 준관성진동의 크기가 다소 과소평가되었을 수도 있으나, 동해 전역에 걸친 준관성진동 시간적 및 공간적 특성을 분석에는 문제가 되지 않는다고 판단하였다. 동해 남부 위도 34.5–35°N 해역에서는 관성주기(21–21.2시간)와 일주기(약 24시간)가 가까워서 두 개의 다른 주기 현상을 분해하기 위해서는 6.9–7.6일의 자료가 필요하다. 본 연구에서는 7일 자료 세트로 구성하였고, 위도 34.5–35°N (대한해협)의 필터링된 값에는 관성주기와 일주기가 다소 섞여 있을 수 있다. 본 연구에서는 관성주기와 일주기가 비교적 원활하게 구분되는 35°N 이상의 해역에서의 준관성진동을 중점적으로 분석하였다. 준관성진동 크기(|u→|)는 준관성주기로 대역통과(band-pass filtering)한 동서 및 남북 방향 유속 ui와 vi의 절대값, |u→|=ui2+vi2으로 계산하였다.

준관성진동을 야기하는 바람에너지 유입(wind energy input, WI)은

로 추정할 수 있다(Crawford and Large 1996; Furuichi et al. 2008; Large and Crawford 1995). τI→는 유속과 동일한 15–23시간의 밴드주기를 적용한 바람응력(wind stress)으로 τ=CDρairU10|U10|로 계산하였다. CD는 항력계수(drag coefficient)로 Donelan (2018)에 제시된 값을 활용하였고, ρair는 공기 밀도 1.2 kg m^-3, U10은 ECMWF에서 제공되는 해수면 10 m 위의 풍속을 표층뜰개의 시간과 위치에 맞춰 보간한 값이다. 바람에너지 유입뿐만 아니라 해양 배경장이 준관성진동에 미치는 영향을 분석하기 위해, 지형류로 산출된 상대와도 역시 표층뜰개의 시간 및 위치에 맞춰 보간하였으며, 이를 바탕으로 준관성진동, 바람에너지 유입, 그리고 배경장 간의 상호 관계를 조사하였다.

태풍이 준관성진동 생성에 얼마나 영향을 미쳤는지 알아보기 위하여 태풍 영향 기간을 태풍 진입 2일 전부터 통과 8일 후로 설정하였고, 본 연구에서는 27년의 분석기간 동안 동해를 통과한 총 102개의 태풍을 선정하여 분석하였다. 동해 계절은 1–3월이 겨울철, 4–6월은 봄철, 7–9월은 여름철, 10–12월은 가을철로 분류되기도 하며, 태풍의 북상은 7–9월에 많다. 이와 같은 이유로 사계절로 나누어, 준관성진동 특징을 살펴보았다.

혼합층 준관성진동 크기 변화는 바람 강제력과 혼합층 두께, 감쇠계수 등의 관계로 설명될 수 있다(Pollard and Millard 1970; D’Asaro 1985). 기존 연구를 보다 간소화하여 월평균 준관성진동 크기를 바람에너지 유입(식 1)의 제곱근(|WI|)과 ORAS5 혼합층 두께의 관계(식 2)로 살펴보았다. 각 변수를 해당 변수의 표준편차 값으로 정규화(normalized)하여 준관성진동 크기(Um)에 미치는 바람 강제력(M)과 혼합층 두께(H)의 영향정도를 비교하였다.

표층뜰개 관측자료는 혼합층 정보를 포함하고 있지 않기 때문에, ORAS5 재분석장의 혼합층 깊이를 이용하였다. ORAS5 재분석장 자료는 Office Hadley Center EN 4.2.1 관측자료가 동화되고 기후월평균 혼합층 두께 변화(Lim et al. 2012)가 잘 재현된다. 표층뜰개 자료로 계산한 준관성진동 크기, 표층뜰개 관측시기 및 위치로 내삽한 바람강제력(바람에너지 유입)과 ORAS5의 혼합층 두께를 기후월평균으로 만들고, 각 변수들은 각각의 표준편차로 정규화하였다.

준관성진동의 e-folding 감쇠시간(e-folding decay time)은 앞서 구성한 표층뜰개 347세트 자료를 다시 300시간(=12.5일) 자료로 재구성하였고, 마지막 구간의 자료가 300시간에 미치지 못하는 경우는 N-299부터 N까지로 구성하였다(N은 임의의 표층뜰개 자료 세트의 마지막 시계열 번호). 재구성한 시계열을 사인함수곡선(sine function curve)에 fitting시켜 준관성진동의 최대 시점부터 e^-1배 되는데 걸리는 시간(감쇠시간)을 계산하였다. 재구성 시계열의 길이가 너무 짧을 경우 적절한 fitting이 불가하므로 최대 시점 이후의 시계열 길이가 72시간(=3일) 이상인 재구성 자료만을 사용하여 감쇠시간을 계산하였다.

3. 결과 및 토의

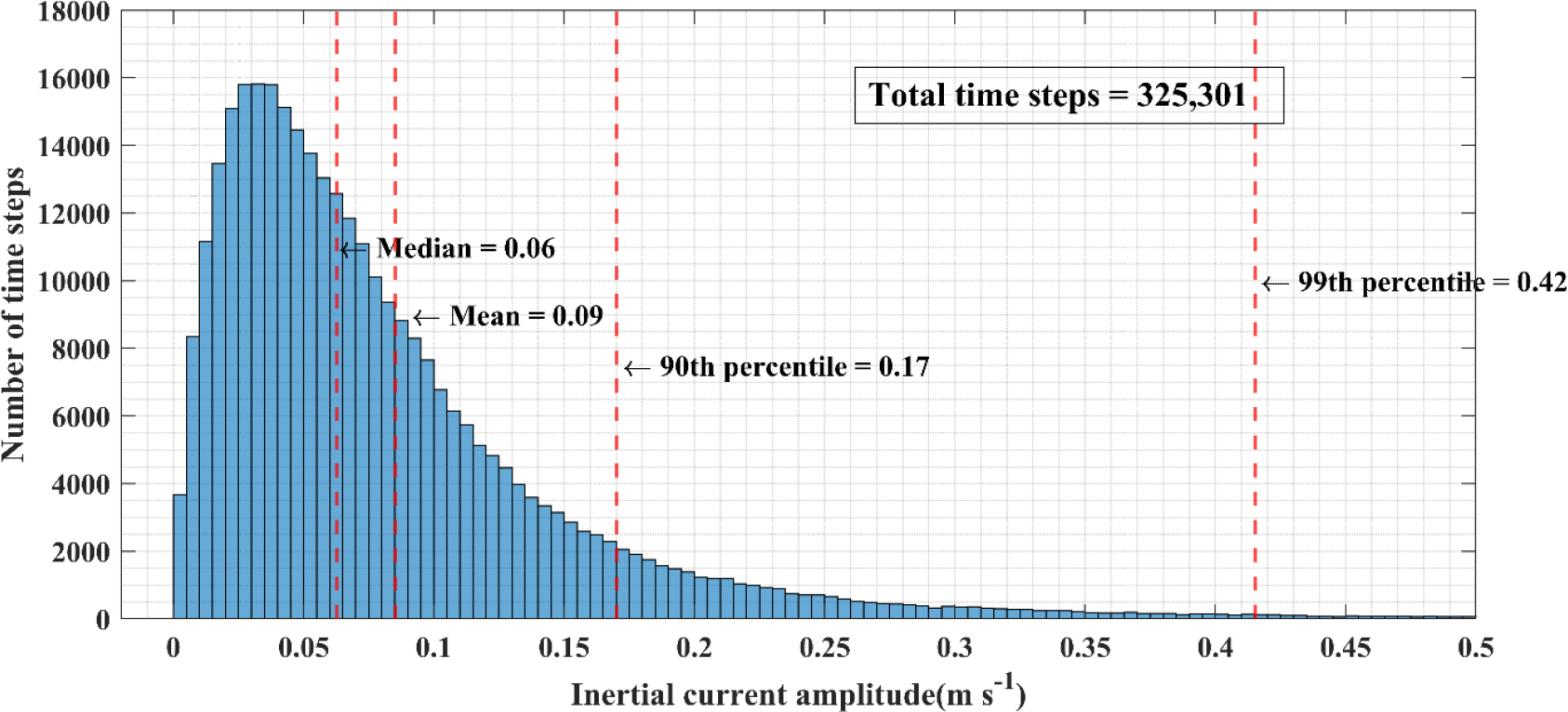
표층뜰개는 공간적으로 동해 남부에 주로 분포하고 있었고, 일본분지 동편과 러시아 연안은 상대적으로 매우 적은 분포를 보였다(Fig. 1). 표층뜰개는 전체 기간 중 2005년에서 2007년 사이에 대부분 집중되어 있었고 2014년과 2018년에는 자료가 존재하지 않았다. 각 분기별로 살펴보면 분기 모두에서 약 150세트 내외로 고르게 분포하였다(Fig. 2). 전체 347세트의 표층뜰개 자료의 총 시간은 325,301시간이고(Fig. 3), 전체 자료 중에서 준관성진동 크기의 중앙값(median)은 0.06 m/s였고, 평균값(mean)은 0.09 m/s로 나타났다. 준관성진동의 최댓값은 1.22 m/s로 나타났으며, 전체 데이터의 90%와 99%가 각각 0.17 m/s와 0.42 m/s 이내에 분포하였다. Park et al. (2004)에서 제시되었던 준관성진동의 중앙값 0.12 m/s과 최댓값 0.4 m/s은 본 자료에 비추어보면 약 90%와 99% 범주에 속하여 기존 값과는 상당한 차이를 보인다. 이는 본 연구에서 사용된 자료가 과거에 비하여 월등히 많아 약한 준관성진동 크기값이 다수 포함되어 중앙값과 평균값이 낮아졌으며, 태풍에 의해 발생한 강한 준관성진동이 포함되어 최댓값은 상승한 것으로 판단된다.

Fig. 3.

Histogram of inertial current amplitude from the total time steps of drifters

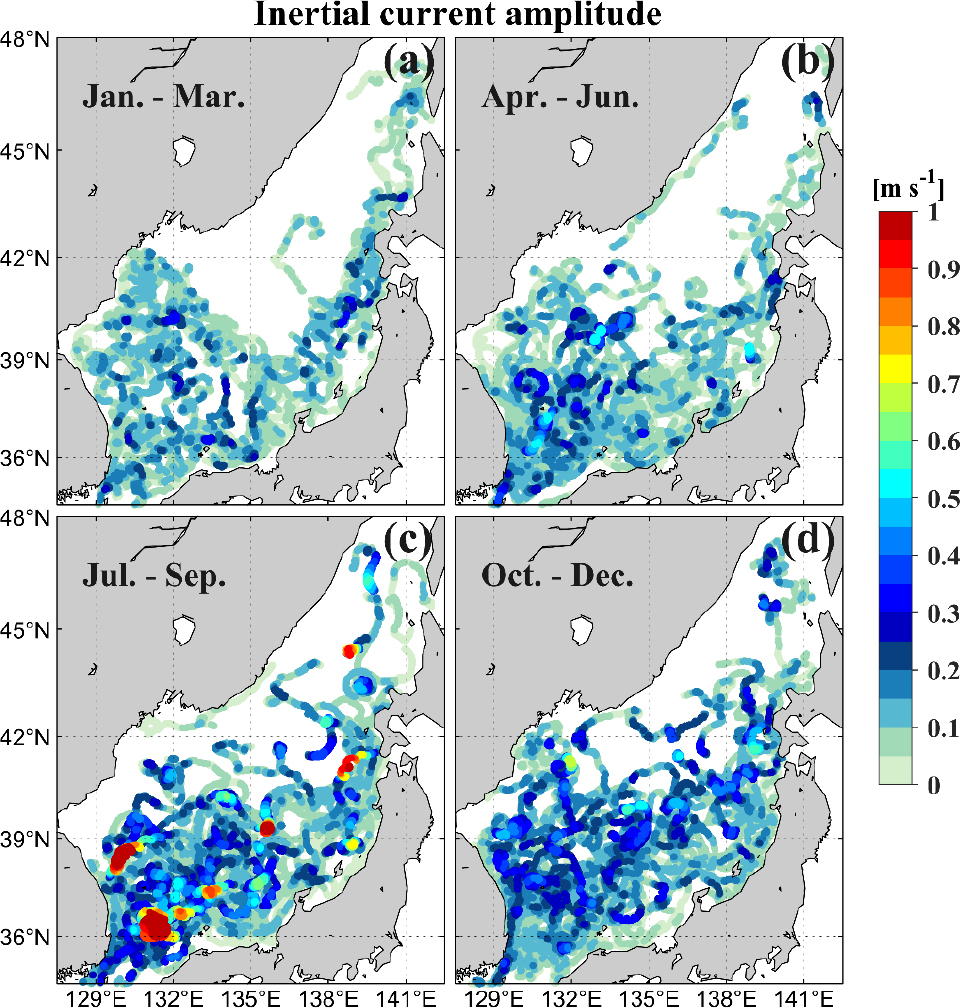
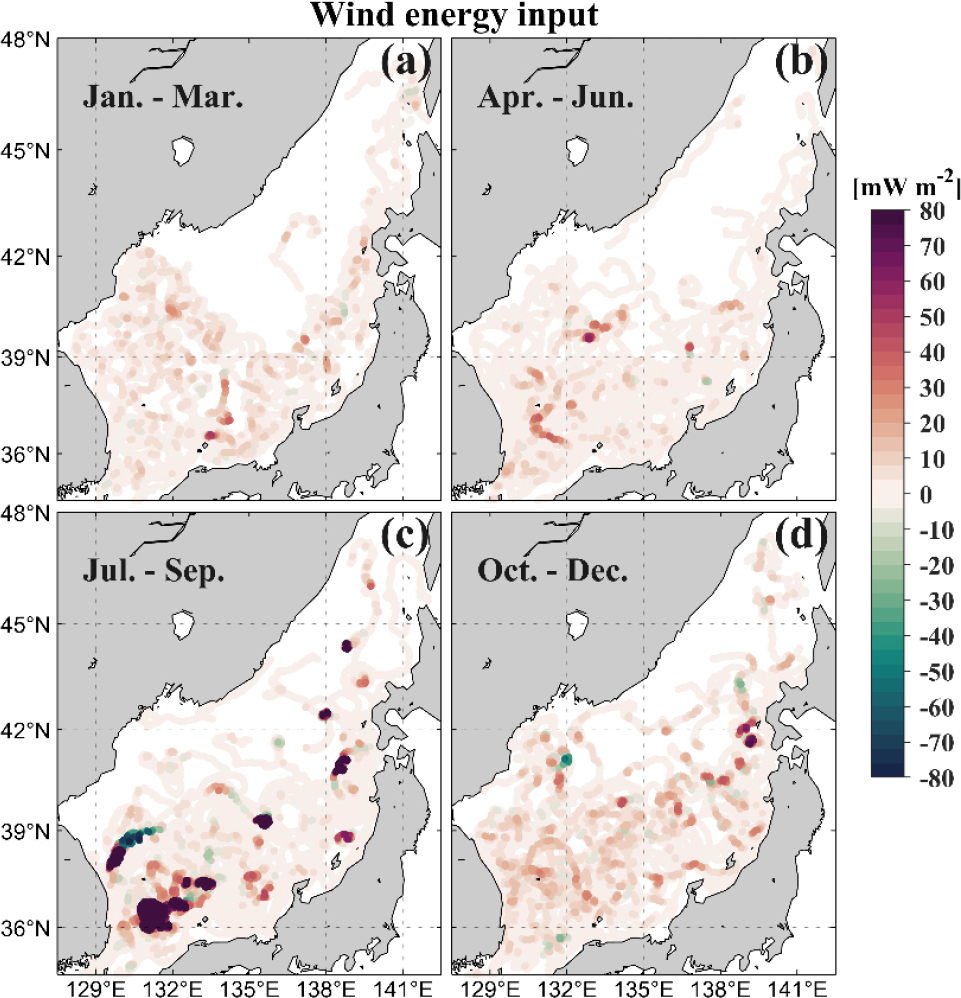
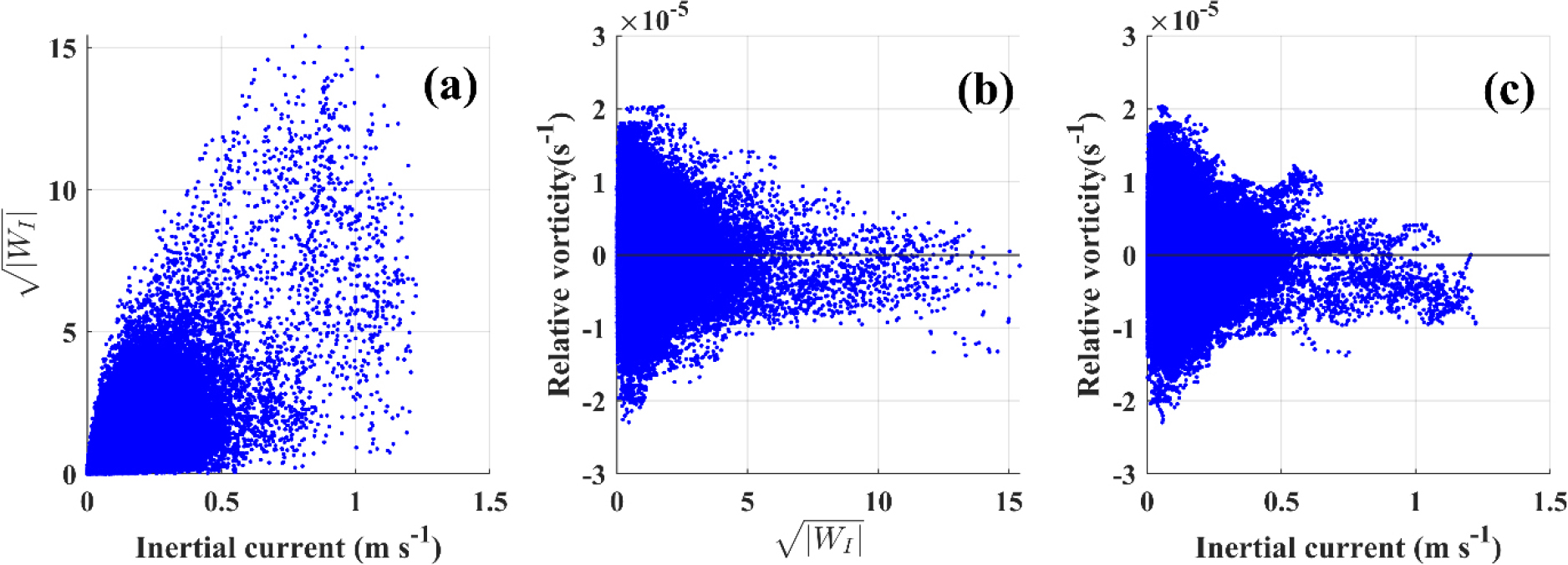
분기별로 나타낸 동해 준관성진동은 여름철(7–9월)에 가장 강하고 가을철(10–12월), 봄철(4–6월), 겨울철(1–3월) 순으로 강하게 나타났다(Fig. 4). 여름철(7–9월)은 0.7 m/s 이상의 강한 준관성진동이 타 시기에 비하여 여러 차례 관측되기도 하였다. 준관성진동을 야기하는 바람에너지 유입은 준관성진동과 마찬가지로 계절 변동성이 보였고, 여름철(7–9월)과 가을철(10–12월)에 전반적으로 강하게 나타났다. 강한 바람에너지 유입이 나타났던 시기와 위치에서 강한 준관성진동이 나타났으며(Fig. 5), Fig. 6a의 산점도(scatterplot)에서도 바람에너지 유입과 준관성진동 크기 사이에 양의 상관관계가 있음을 확인된다. 해류장과 준관성진동을 발생시키는 바람에너지 유입 간의 관계에서는 음의 상대와도(시계방향 회전성)에서 상대적으로 강한 바람에너지 유입이 나타났고(Fig. 6b) 강한 준관성진동도 더 많이 분포하였다(Fig. 6c). 이로부터 표층뜰개에서 관측된 강한 준관성진동의 대부분은 바람-해류 공명에 의해 발생하며, 강한 바람-해류 공명과 강한 준관성진동은 음의 상대와도 영역에서 더 높은 확률로 나타날 수 있다고 여겨진다.

Fig. 4.

The inertial current amplitude observed at each quarter

Fig. 5.

The wind energy input for inertial current at each quarter

Fig. 6.

Scatterplots illustrating the relationships among the inertial current, square root of the wind energy input (|WI|), and relative vorticity: (a) |WI| versus inertial current, (b) relative vorticity versus |WI|, (c) relative vorticity versus inertial current

월별로 계산한 준관성진동 평균값은 9월에 약 0.15 m/s로 최대를, 1–3월에 0.05–0.06 m/s의 범위로 최소를 나타냈다(Fig. 7a). 월별 계산에 활용된 표층뜰개 개수(total bar)는 매월 약 40개 내외로 비슷하였고, 준관성진동 크기가 평균값 0.09 m/s (Fig. 3)보다 큰 값을 보인 뜰개 개수(bars in light cyan)는 가을(9, 10, 11월)에 최대로 나타났다(Fig. 7b). 월별 표층뜰개 개수와 평균값 이상의 크기를 갖는 뜰개 개수 비율을 살펴보면 9, 10, 11월이 가장 높고, 5–8월과 12월이 그 다음, 1–4월이 가장 낮게 나타났다. 이는 동해 표층에서의 상대적으로 강한 준관성진동이 주로 9–11월에 존재하였음을 의미한다.

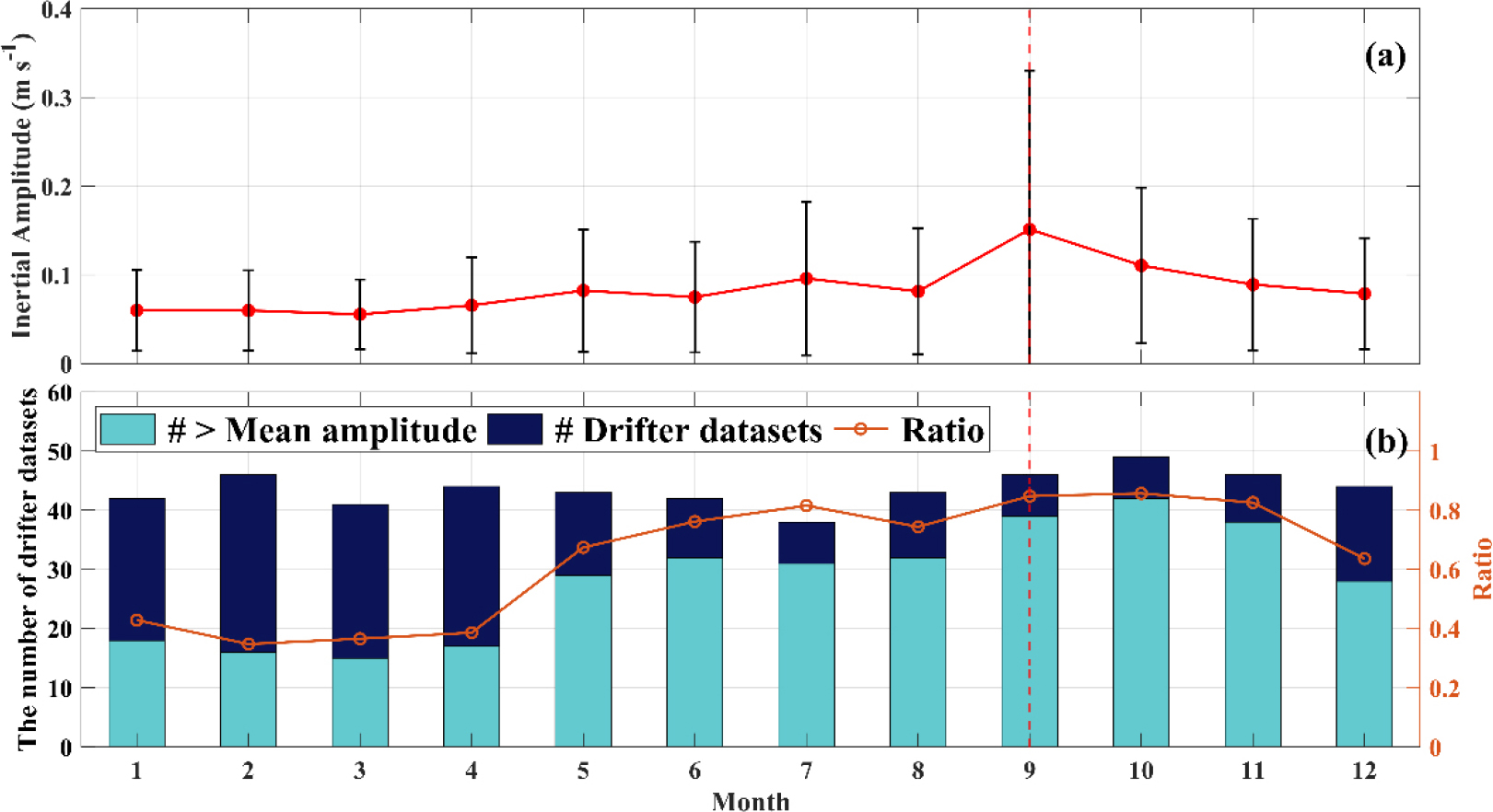
Fig. 7.

(a) Monthly-mean inertial current amplitude in the East Sea calculated from GDP. (b) The total number of drifter datasets for each month (bar), the number of drifter datasets higher than the mean of inertial current amplitude (light cyan bar), and the ratio of the two (orange line with open circle). The month of highest inertial current amplitude and ratio is indicated with red dashed line

표층뜰개에서 나타난 준관성진동 최대 시기는 9월로 Jeon et al. (2019)에서 제시된 11–12월과 차이를 보인다. 연구 기간의 차이도 하나의 원인일 수 있으나, 혼합층 두께 변화를 고려하여 생각해볼 수 있다. 기존 Jeon et al. (2019)연구는 혼합층 내 에너지 합을 계산하여 11월과 12월이 최대라는 결과를 얻었으나, 표층뜰개에서 얻어진 준관성진동은 일정 수심(약 15 m)의 유속(m/s)이다. (식 2)의 혼합층 운동량 보존에 관한 유속-두께의 관계(Um=MH-1)로 부터, 깊은 혼합층이 나타나는 11월과 12월은 혼합층 내 에너지가 9월보다 크더라도 혼합층 내 준관성진동의 크기(유속)는 작아질 수 있고, 그 결과 표층뜰개에서의 준관성진동의 최대가 11–12월이 아닌 혼합층이 얕은 9월에 나타나게 하는 원인일 수 있다.

표층뜰개에서 관측되는 준관성진동 크기의 시간적 및 공간적 변동성은 바람-해류 공명과 혼합층 두께와 관련되어 있고, 각 인자에 의한 영향도를 평가해 볼 수 있다(Park et al. 2005). 본 연구에서는 드로그가 존재하는 표층뜰개만을 활용하여 바람의 빠른 변화에 의한 효과보다는 바람-해류 공명에 의한 효과가 가장 지배적이었으며, 동한난류와 같은 강한 해류역에서도 타 해역과 다른 특이한 준관성진동 특성을 두드러지지 않았다.

준관성진동 변동성에 미치는 바람에너지 유입(=바람-해류 공명)과 혼합층 두께의 영향을 살펴보기 위하여, 기후월평균 준관성진동을 U(검은실선 Uo와 회색실선 Um), 기후월평균 바람강제력을 M(파란 실선), 기후월평균 혼합층 두께를 H(빨간 실선)로 표시하였다(Fig. 8). 혼합층 재분석장을 표층뜰개 관측시기 및 위치로 내삽하여 계산한 월평균 혼합층 수심은 1월 90 m, 2월 96 m, 3월 76 m, 4월 35 m, 5월 16 m, 6월 11 m, 7월 11 m, 8월 11 m, 9월 18 m, 10월 32 m, 11월 53 m, 12월 76 m로 나타났으며, 표준편차는 33 m였다. Uo는 표층뜰개에서 관측된 값이고, Um는 (식 2)로 계산한 값이다. Uo는 바람에너지 유입 M과 동일하게 9월에 최대를 보였고, 혼합층 두께 변화가 작은 1–2월, 5–10월에는 Uo와 M이 동일한 증감 경향을 보였다. 그러나 혼합층 두께 변화가 커지는 3–4월, 10–12월은 M의 증감 경향과 Uo의 경향이 일치하지 않았고, 혼합층이 깊을수록 같은 크기의 바람에너지 유입이라도 Uo가 작게 나타났다. M과 H로 계산한 준관성진동 크기 Um(식 2)은 5–8월 사이의 변동성과 9월의 최댓값, 그리고 혼합층이 깊어짐(얕아짐)에 따라 감소(증가)하는 Uo의 변동성이 그대로 표현되어 표층뜰개의 준관성진동의 변동성이 바람에너지 유입과 혼합층 두께 변화로 잘 설명됨을 확인할 수 있었다.

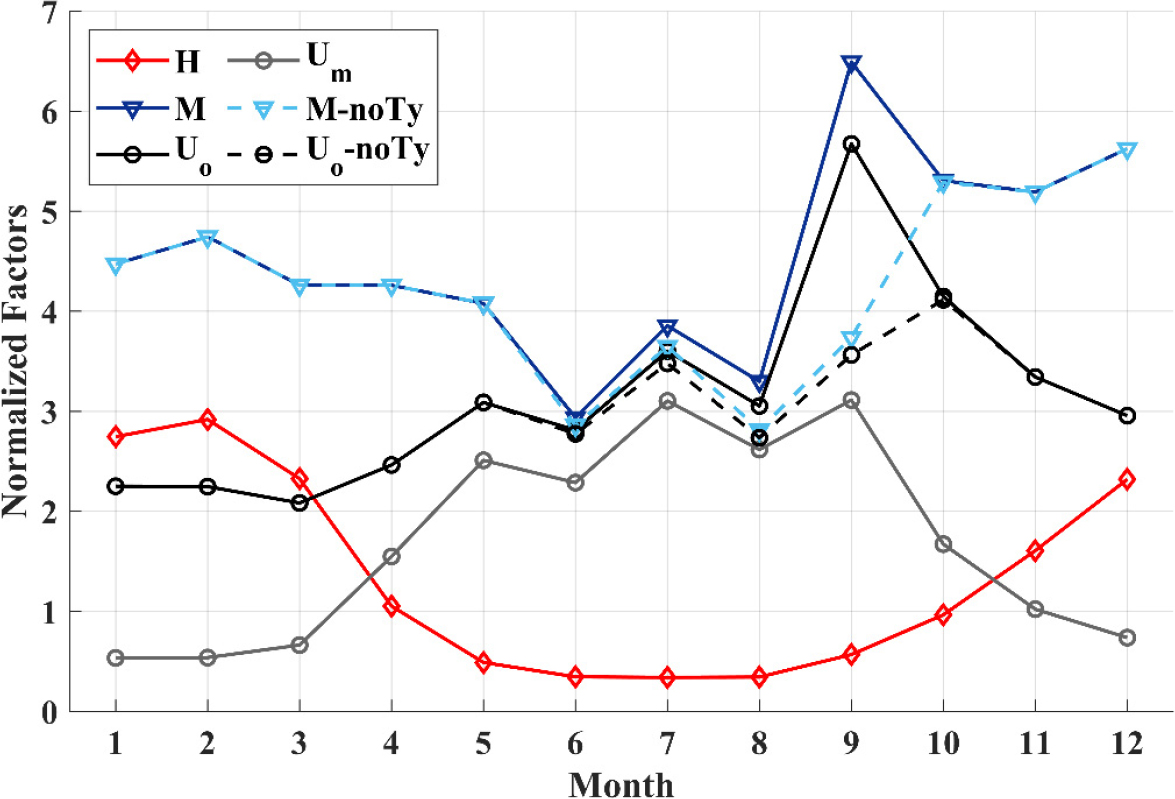
Fig. 8.

Monthly variation of the normalized inertial amplitude (Uo, solid black line), mixed layer depth (H-1, solid red line), and inertial momentum (M, solid blue line) (=square root of the wind energy input). UM is the calculated normalized inertial amplitude through MH-1, solid gray line.) M-noTy (dashed sky blue line) and Uo-noTy (dashed black line) are the same as M and Uo except for the effect of typhoon, respectively

한편 혼합층이 깊게 발달하는 겨울철의 Um은 전반적으로 Uo보다 작고 변동성도 작게 나타났다. 이는 실제로는 준관성진동이 혼합층 내에서 연직적으로 균등한 크기일 것이라는 가정의 Um과는 달리, 겨울철 두터운 혼합층 내에서 표층 부근의 준관성진동이 더 강하고, 깊어질수록 약해지는 불균등성이 주된 요인일 것으로 추측된다.

태풍은 강한 준관성진동을 발생시키는 요인 중 하나로, 수치모형을 활용한 기존 연구에서는 동해를 통과하는 태풍에 의해 야기된 준관성진동이 겨울철 강한 바람에 의한 준관성진동과 비슷한 수준일 수 있다고 하였다(Song et al. 2020). 표층뜰개 자료에서 태풍 영향 기간을 선별하여(방법 참조) 준관성진동의 특성을 살펴보았다(Fig. 9a). 전체 표층뜰개 자료 325,301시간 중에서 29,508시간의 자료가(약 9%) 태풍 영향 기간에 해당하였고, 표층뜰개 자료에 기록된 월별 태풍 영향시간의 총합은 7월에 3,975시간, 8월에 9,839시간, 9월에 10,774시간, 10월에 2,536시간, 그 외 기간에 2,384시간으로 대부분(70%)이 8월과 9월에 집중되어 있었다. 전체 준관성진동 크기 중 평균보다 큰 값의 15%가, 상위 10%이상의 값(> 0.17 m/s) 중 24%가, 상위 1% 값(> 0.42 m/s) 중 61%가 태풍 영향 기간에 해당하였다(Fig. 9b). 이로부터 동해의 강한 준관성진동의 상당 부분이 태풍에 의한 것임이 확인된다. 더불어 위의 모든 범주(평균, 상위 10% 이상, 상위 1%)에서 9월의 비중이 가장 높게 나타나 강한 준관성진동일수록 9월에 분포하고 있을 가능성이 높다고 생각된다(Fig. 9b, 노란색 막대그래프). 이를 확인하기 위하여 태풍 영향 기간에 해당하는 자료를 제외한 준관성진동 크기(Uo-noTy, 검은색 파선), 바람에너지 유입(M-noTy, 하늘색 파선)을 다시 재계산하였고, 태풍 영향 기간을 제외하지 않은 기존 각 변수들의 표준편차로 정규화하였다(Fig. 8). 태풍 영향 기간을 제외한 바람에너지 유입 M- noTy는 9월에 나타나던 최댓값이 10, 11, 12월로 바뀌고 계절 변동성이 두드러지게 변하였다. 표층뜰개에서 획득된 준관성진동 크기 Uo-noTy의 최댓값도 9월이 아닌 10월로 옮겨갔다. 이로부터 태풍에 의한 영향이 9월에 가장 크고, 그로 인하여 가장 강한 준관성진동이 9월에 집중되어 있음을 확인하였다. 또한 태풍에 의한 바람에너지 유입을 제거한 결과로부터, 계절 몬순에 의한 바람에너지 유입과 혼합층 두께 변화가 준관성진동의 계절 변동성의 주요 요인임이 확인되어 Jeon et al. (2019)에서 제시된 내용과 일치하였다.

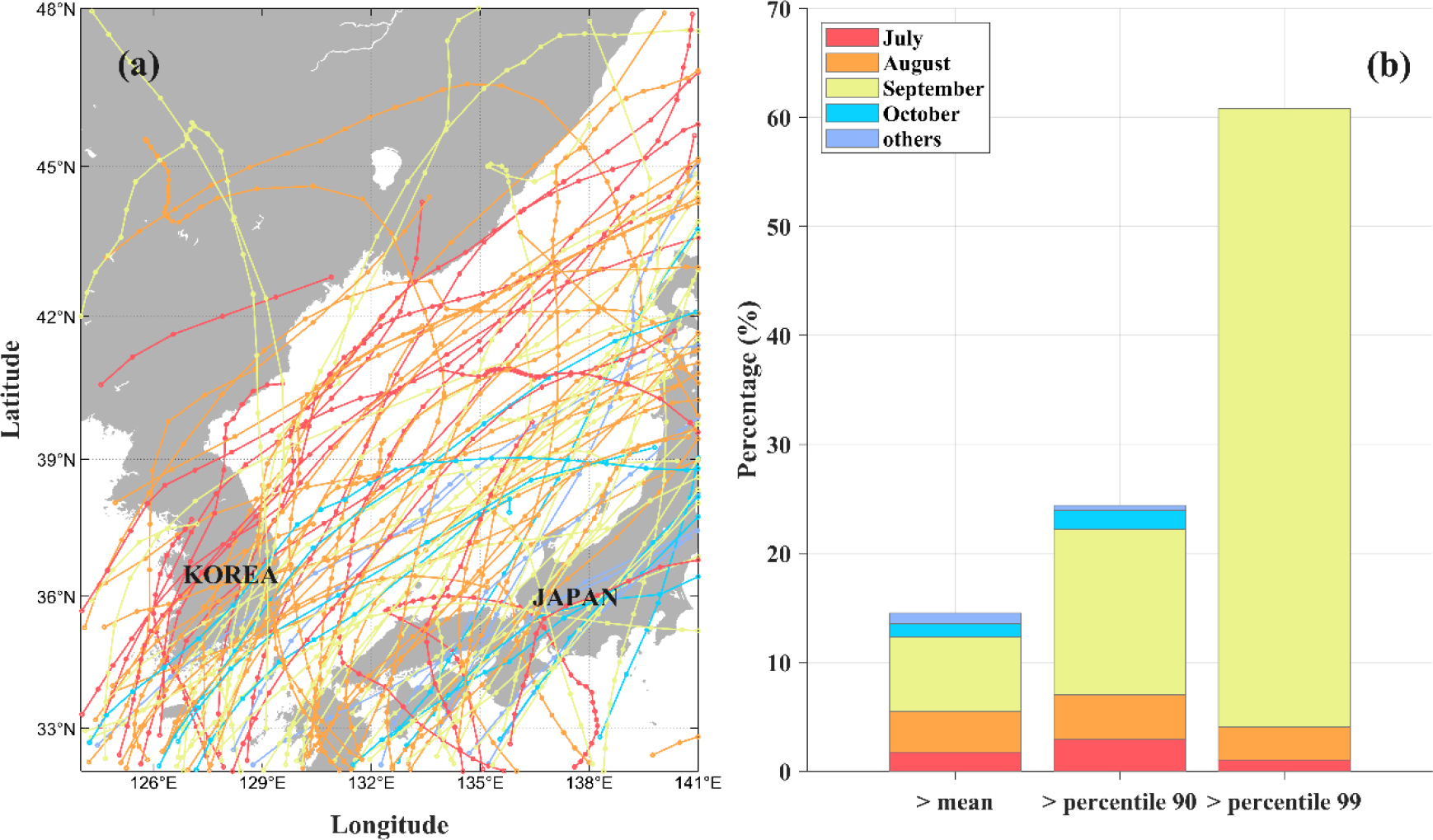
Fig. 9.

(a) Tracks of typhoons for 27 years (July in red, August in orange, September in yellow, October in cyan, and others in sky blue). (b) Percentage of the typhoon influence period overlapping values above the median, top 10% and top 1% in the histogram of Fig. 3, shown as stacked bars by month

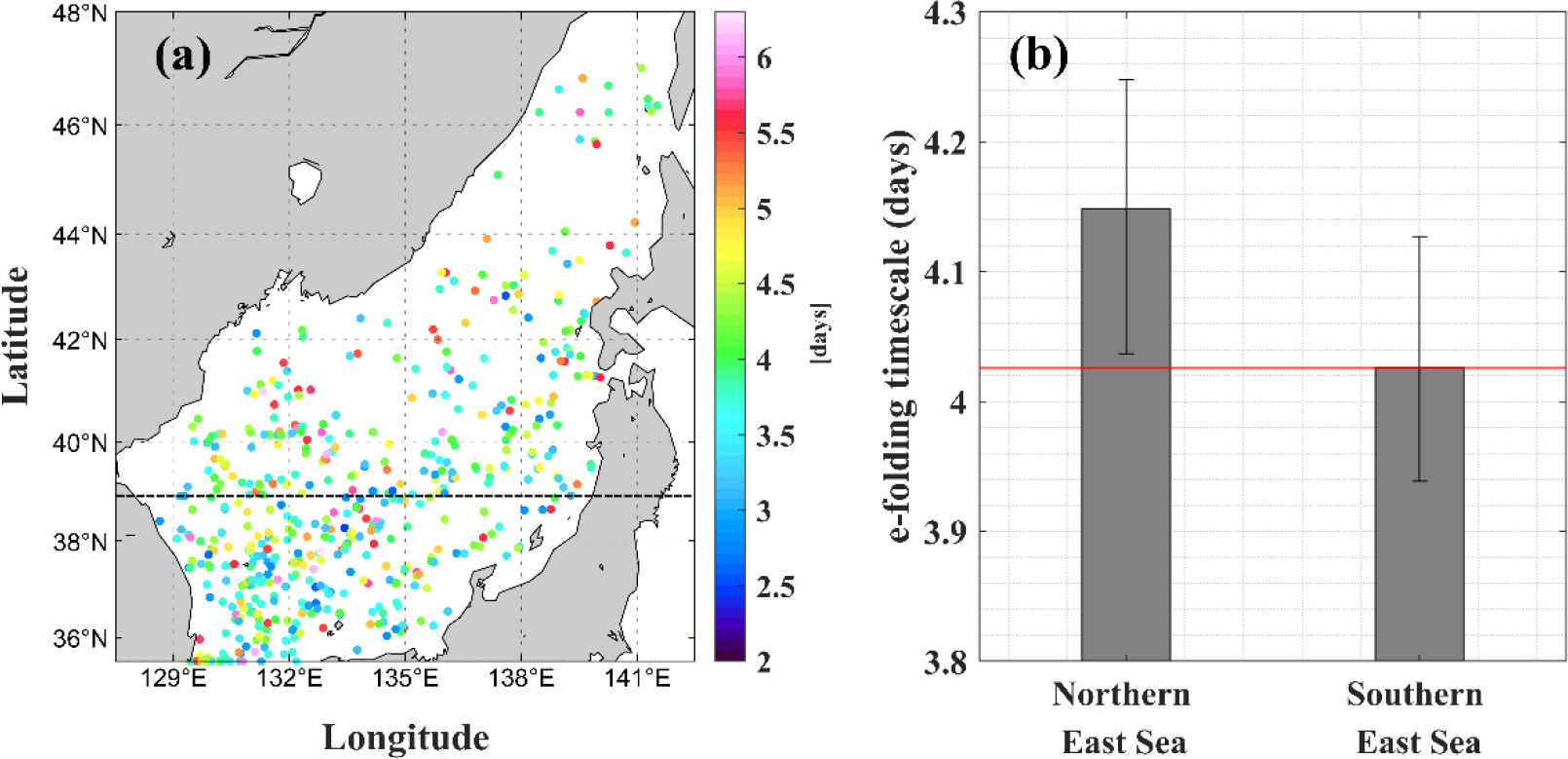
준관성진동 감쇠시간은 에너지의 수평 및 수직 방향 전파 및 소산에 의해 결정된다. 기존 연구에서는 관성진동 감쇠시간규모를 2–10일 정도로 제안하였으며(D’Asaro 1985), 북태평양 고위도 해역을 제외하면 대개 4일 내외로 평가되었고(Park et al. 2009), 준관성진동 생성과 소멸 과정 연구에 활용되는 slab model의 감쇠시간규모도 일반적으로 4일 내외의 값이 사용되고 있다(e.g., Park et al. 2010). 동해 3차원 해양순환모형에서 재현된 준관성진동의 감쇠시간도 약 4일 내외의 값을 보이나(Jeon et al. 2019), 장기간 관측자료 기반의 동해 준관성진동 감쇠시간규모의 통계적 수치는 아직 명확하게 제시된 바 없다. 장기간 표층뜰개 자료로 계산한 동해 준관성진동의 감쇠시간은 약 4일 내외로 나타났고(Fig. 10), 기존 연구에서 제안 및 사용되는 값과도 유사하였다. 표층뜰개 자료는 동해 북부 일본분지에서 상대적으로 매우 적었지만, 아극전선의 대략적인 위도 39°N를 경계로 남부와 북부의 감쇠시간을 비교하였을 때, 39°N 이북은 약 4.15시간, 이남은 약 4.02시간으로 동해 북부가 0.13시간 더 길게 나타났다. 이는 동해 북부에서 발생한 준관성진동은 혼합층 내에서 동해 남부보다 더 길게 유지될 수 있음을 의미하며, Jeon et al. (2019)에서 제시된 동해 남부에서의 더 큰 음의 상대와도로 인한 표층 준관성진동 에너지가 중층 및 심층으로 더 빠르게 전달되는 결과와 일치한다.

Fig. 10.

(a) Decay timescale of near-inertial oscillation (NIO) in the East Sea. The gray dashed line represents the latitude of 39°. (b) Mean decay timescale in northern and southern regions of the East Sea. Error bar indicates 95% confidence interval

본 연구를 통하여 준관성진동 크기의 계절 변동성은 확인되었으나, 계절적 감쇠시간의 유의미한 차이를 확인하기에는 자료가 충분하지 않았다. 또한 수백 m의 깊은 혼합층을 형성하는 심층대류(deep convection)가 발생하는 해역(러시아 앞바다 및 일본분지 북부)은 표층뜰개가 상대적으로 거의 분포하지 않아서 Jeon et al. (2019)에서 제시된 준관성진동의 빠른 감쇠도 확인하기 어려웠다.

4. 요약 및 결론

현재까지 다양한 관측 및 수치모형자료를 이용한 동해 준관성진동에 대한 연구가 이루어졌으나 장기간 실측자료에 기반한 준관성진동의 시간적 및 공간적 분포와 특성에 대한 연구가 이뤄지지 못하였다. 본 연구에서는 동해 전 영역에 준하는 영역의 총 27년간의 1시간 간격의 고해상도 GDP 표층뜰개 관측자료를 활용하여 표층 준관성진동의 특징을 확인하고 재고찰하였다.

표층뜰개 자료에서 얻어진 동해 준관성진동의 중앙값은 0.06 m/s였고, 평균값은 0.09 m/s였다. 준관성진동은 여름철(7–9월)과 가을철(10–12월)이 겨울철(1–3월)에 비하여 강하게 나타났으며, 특히 여름철(7–9월)은 다른 분기보다 더 강한 준관성진동이 관찰되었다. 준관성진동을 야기하는 바람에너지 유입(바람-해류 공명)은 준관성진동과 마찬가지로 여름철(7–9월)과 가을철(10–12월)에 전반적으로 강했으며, 강한 준관성진동이 나타나는 곳에서 바람에너지 유입이 크게 나타나 표층뜰개에서 관측된 강한 준관성진동의 에너지원은 바람-해류 공명이 주된 요인임을 확인하였다. 준관성진동의 감쇠시간은 약 4일 내외로 나타나 slab model에서 사용되는 4일의 감쇠시간규모가 적절함을 알 수 있었다. 또한, 동해 북부에서의 감쇠시간이 유의미하게 남부보다 길게 나타나, Jeon et al. (2019)에서 보고된 동해 북부의 더 긴 감쇠시간 계산 결과를 뒷받침하였다.

월별 준관성진동의 크기 비교는 9월이 최대, 3월이 최소를 보였고 0.05–0.15 m/s 범위에서 나타났다. 9월이 최대로 나타난 원인은 가장 강한 바람에너지 유입과 얕은 혼합층 때문이었고, 강한 바람에너지의 상당 부분은 태풍 기원의 바람이었다. 이는 Song et al. (2020)에서 언급된 결과와 일치하며, 태풍이 동해 준관성진동의 상당한 에너지원이며, 가을철의 강한 준관성진동 크기와 비슷한 수준이거나 그 이상임을 확인하였다.

본 연구는 장기간의 표층뜰개 관측자료만을 이용하여 동해 표층 준관성운동의 시간적 및 공간적 특성을 산출하였다는 의미가 있다. 그러나 표층뜰개 관측자료가 일본분지 북부와 러시아 연안에서 매우 부족하였고, 연도별로도 고르게 분포하지 않아서 Jeon et al. (2019)에서 제시된 준관성진동의 특성을 모두 재확인하는 데에는 한계가 있었다. 한 시간 간격의 고해상도 표층뜰개 관측자료가 동해 북부의 빈 영역을 메우며 장기간에 걸쳐 축적된다면, 동해의 지역적 및 시기별 준관성진동의 특성을 보다 면밀히 검토할 수 있을 것으로 기대된다.