1. 서 론
유체동력 터빈(hydrokinetic turbine)은 조석에 의한 흐름이나 하천의 흐름에 의해 로터(rotor)를 회전시킴으로써 전기 생산에 사용되는 수중 기계 장치이다. 원리는 풍력발전 터빈과 같이 유체의 운동에너지로부터 터빈 회전 에너지로 변환하여 발전하나 물의 밀도가 공기의 밀도보다 훨씬 높기 때문에 같은 시설용량인 경우 유체동력 터빈의 직경이 훨씬 작다. 또한 물의 흐름을 이용한 유체동력 발전은 계절이나 날씨에 영향을 거의 받지 않아 연속적인 발전이 가능하고 예측이 가능하며 환경문제가 적다는 장점이 있다. 유체동력 터빈의 국내 실증 연구로서 진도와 해남 사이의 울돌목 협수로에 위치한 시험조류 발전소에서 나선형 블레이드의 수직축 조류터빈에 대한 실증 실험이 2000년대 초반에 수행되었다(Han et al. 2013). 최근 국내 연구로는 한국해양과학기술원에서 200 kW급 수평축 터빈 개발 및 실증 연구를 수행하였으며(Ko et al. 2019) 동일 연구 기관에서 100 kW급 수직축 터빈에 에너지저장장치를 결합하는 도서지역 보급 모델을 개발하여 실증 중에 있다.
유체동력 터빈(hydrokinetic turbine)은 조석에 의한 흐름이나 하천의 흐름에 의해 로터(rotor)를 회전시킴으로써 전기 생산에 사용되는 수중 기계 장치이다. 원리는 풍력발전 터빈과 같이 유체의 운동에너지로부터 터빈 회전 에너지로 변환하여 발전하나 물의 밀도가 공기의 밀도보다 훨씬 높기 때문에 같은 시설용량인 경우 유체동력 터빈의 직경이 훨씬 작다. 또한 물의 흐름을 이용한 유체동력 발전은 계절이나 날씨에 영향을 거의 받지 않아 연속적인 발전이 가능하고 예측이 가능하며 환경문제가 적다는 장점이 있다. 유체동력 터빈의 국내 실증 연구로서 진도와 해남 사이의 울돌목 협수로에 위치한 시험조류 발전소에서 나선형 블레이드의 수직축 조류터빈에 대한 실증 실험이 2000년대 초반에 수행되었다(Han et al. 2013). 최근 국내 연구로는 한국해양과학기술원에서 200 kW급 수평축 터빈 개발 및 실증 연구를 수행하였으며(Ko et al. 2019) 동일 연구 기관에서 100 kW급 수직축 터빈에 에너지저장장치를 결합하는 도서지역 보급 모델을 개발하여 실증 중에 있다.
유체동력 터빈은 블레이드의 항력 또는 양력을 이용하여 발전하게 되며 수평 또는 수직 축 터빈을 포함하여 여러 유형으로 개발되고 있다. 이 중 수평축 터빈(Horizontal Axis Turbine, HAT)은 가장 효율적인 유체동력 터빈으로 알려져 있다. 실험실 규모의 HAT 실험 연구에서 달성된 출력 계수가 48%로 높은 효율성이 확인되었다(Batten et al. 2007). 반면 HAT보다 다소 낮은 효율을 보이고 있지만 수직축 터빈(Vertical Axis Turbine, VAT)은 모든 흐름 방향으로 작동 할 수 있는 장점을 가지고 있다. VAT 중 양력 유형인 다리우스 터빈(Darrieus turbine)의 경우 직선 블레이드를 갖는 모형에 대한 실험 수행에서 최고 효율 30%를 달성한 바 있다(Li and Calisal 2000a). 하천이나 수로에서의 흐름을 이용하는 경우의 유체동력 터빈은 이미 상용화가 되었으며 수평축의 경우 독일의 Smart Hydro Power사, 수직축 터빈의 경우 미국의 Emrgy사의 제품이 대표적이다. 조류발전에 사용되는 경우 현재 상용화는 우수한 효율을 보이는 수평축 터빈 위주로 진행되고 있지만 조류 방향의 변동성이 크거나 유향 제어를 제외하여 복잡성을 낮추고자 하는 경우에 다리우스 터빈이 대안으로 개발되고 있으며 도서지역 보급 시 해안 근처에 적용도 가능하여 다리우스 터빈 관련 연구가 지속되고 있다.
다리우스 터빈의 성능 향상 노력 중에는 상호작용의 긍정적인 효과를 얻기 위해 두 개의 터빈을 동시에 활용하는 방식인 쌍동 터빈(twin turbine)에 대한 연구가 있다. 세 개의 블레이드를 갖는 수직축 쌍동 터빈을 근접 배치하였을 때 단일 터빈 두 개 효율의 합보다 25% 정도 향상됨을 확인하였고, 같은 방향과 반대 방향으로 회전하는 경우의 최적인 조합을 제안하였다(Li and Calisal 2000b). 또한 네 개의 블레이드를 갖는 수직축 쌍동 터빈의 근접 배치의 경우에도 단일 터빈 두 개 효율의 합보다 24% 향상됨을 확인하였고, 반대 방향으로 회전하는 경우의 최적 조합을 제시하여 공간 활용 및 효율 향상이라는 장점을 얻을 수 있는 가능성을 보였다(Khalid et al. 2013). 또한 이어지는 실험 연구(김 등 2019)에서도 실해역 사이트에서 단일 터빈 대비 16.6%의 효율 향상 결과를 보고하였으며 규모를 증가하고 익형 지지대를 고려한 쌍동 터빈 해석에서 127 kW의 출력과 26.6%의 효율(허 등 2020)을 얻을 수 있었다.
다른 효율 향상 방안 중 덕트(duct) 형태를 이용한 유속 강화 연구는 수평축 터빈에서 먼저 진행되었다. 이 중 출구 쪽 확산 효과를 이용한 방식은 최근에도 연구가 이어지고 있으며 최적 형상을 도출하기 위한 실험적(Ambarita et al. 2022) 그리고 수치적(Liu et al. 2023) 연구 결과들이 발표되었다. 출구 쪽 확산 효과를 이용한 덕트는 단일 다리우스 터빈에도 적용되어 효율 향상을 확인할 수 있었다(Kirke 2011; Amarta and Ismail 2021). 쌍동시스템에 대해서는 고정식 덕트와 효율 향상에 대한 국내 수치해석 연구(허 등 2021)도 보고 되었으며 유사한 구조의 시스템에 대한 영국에서 수행된 실험 연구도 발표되었다(Runge et al. 2018). 하지만 출구 쪽으로 나오는 유동의 확산을 가져오는 확산기(diffuser)를 설치하게 되면 방향성을 가지게 되어 방향이 바뀌는 조류에서 에너지를 추출할 때 유향 의존성이 없는 다리우스 터빈의 장점이 사라질 수 있게 된다.
따라서 본 연구에서는 다리우스 유체동력 터빈의 효율 향상에 활용되는 상호작용과 확산 효과에 따른 성능 향상 정도를 확인해 보고자 하며 유향 변화에 대한 대응 방법을 제시하고자 한다.
2. 재료 및 방법
다리우스 터빈 및 덕트
다리우스(Darrieus) 터빈
양력을 활용하는 다리우스 터빈 제원과 유동해석 조건은 Fig. 1과 Table 1에 각각 나타내었다. 수조에서의 모형 실험 검증용으로 실제 모형보다 축소된 직경 300 mm의 터빈을 선정하였고 자세한 제원은 Table 1과 같다. 이전 블레이드 피치와 캠버(camber)의 효과를 보기 위한 실험 연구(고 등 2019)에서도 직경 300 mm 터빈이 사용되었고, 다리우스 터빈의 상호작용 효과를 보기 위한 실내 실험에서는 직경 150 mm 터빈이 사용된 바 있어(김 등 2019), 본 연구에서는 300 mm를 채택하였다. 터빈의 원주 대비 블레이드가 차지하는 비율을 나타내는 형상 설계 변수인 솔리디티(solidity)도 이전 연구(고 등 2019)에서 사용한 0.2785를 채택하였고 블레이드 개수도 동일한 3개를 사용하였다.
Table 1.
Specification and analysis condition of the Darrieus turbine
| Blade airfoil of turbine | NACA0020 |
| Chord length, C (mm) | 87.5 |
| Number of blades, B | 3 |
| Solidity, S () | 0.2785 |
| Radius of turbine, R (mm) | 150 |
| Velocity, V (m/s) | 0.6 |
효율 개선을 위해 한 개의 터빈을 유향에 수직한 방향으로 Fig. 2와 같이 추가하였다. 이를 쌍동 구성(twin configuration)이라 명명하며 이때의 격자시스템도 Fig. 2에서 확인할 수 있다. 쌍동 구성 터빈의 성능에 영향을 미치는 주요 요인인 터빈 회전 방향, 터빈 간 거리, 터빈 간 위상차를 다르게 하면 효율이 달라질 수 있다. 쌍동 터빈의 최적 조합에 대한 수치 연구에서는 두개의 단일 터빈 효율 합에 비해 25% 정도의 효율향상을(Li and Calisal 2000b), 최적 설계된 쌍동 터빈의 실외 실험 연구에서는 16.6%의 효율향상이 있었음(김 등 2019)이 보고된 바 있다.
덕트(duct)
덕트는 터빈에 입사되는 유속을 증가시키는 목적으로 사용되며 입구와 출구의 대칭형과 비대칭 확산형으로 구분된다. 본 연구에서는 이 두가지 형태가 쌍동 터빈의 효율에 미치는 효과를 해석하고자 한다. 먼저 대칭형 덕트로는 Fig. 3과 같이 단순한 사다리꼴 형태로 각도를 달리하며 효과를 확인해 보고자 한다. 격자 시스템은 각도 10°에 대한 경우를 나타내었고 다른 각도도 같은 수준으로 격자 시스템을 생성하였다.
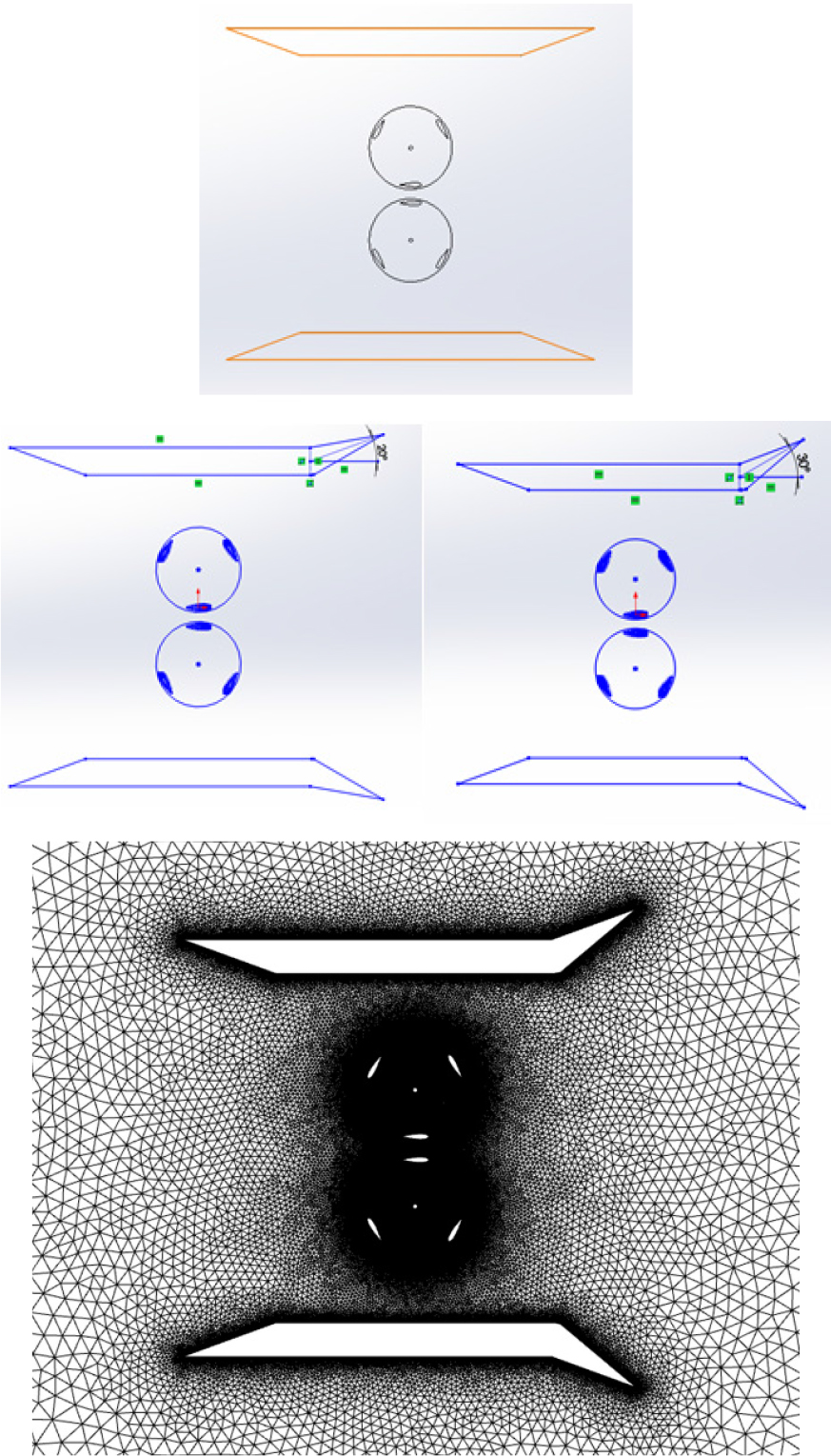
출구 쪽으로 나가는 유체의 확산을 유도하는 비대칭형 덕트는 단순 사다리꼴 형태에서 출구 쪽 각도를 조절하는 방식으로 Fig. 4와 같이 형식을 변경하였다. 출구 쪽 확산 효과가 커질수록 입구로의 유동의 유입이 더 커질 것으로 예상할 수 있고 각 경우의 형상과 격자 모양은 Fig. 4에서 확인할 수 있다. 격자 시스템은 각도 30°에 대한 경우를 나타내었고 다른 각도도 같은 수준으로 격자시스템을 생성하였다.
해석 방법과 성능 평가 수치
상용 프로그램인 ANSYS FLUENT를 사용하며 유한부피법을 이용한 나비에-스톡스 방정식의 해를 얻는 방식으로 유동 해석을 수행한다. 압력 기반 레이놀즈 평균 나비에-스톡스 모델은 비정상적인 조건에서 유체 특성을 계산하는 데 사용된다. 회전하는 터빈을 포함하는 내부 회전 도메인에서 외부 도메인으로 유체 매질을 이동하기 위해 슬라이딩 메쉬 방법을 사용하였다. 벽면 근처에서 k-w 모델의 이점과 벽면 이외에서 k-𝜀 모델의 이점을 결합한 SST (Shear Stress Transport) k-w 난류 모델을 선택하였다. SST k-w는 강한 역기울기(adverse gradient) 및 터빈 시뮬레이션에서 분리 흐름을 가진 유동에서 우수한 결과를 제공하는 것으로 알려져 있다(Dai et al. 2010). 압력 이산화 및 운동량에 대해 각각 2차 정확도 모델 및 2차 업윈드(upwind) 모델을 선택하였다. 또한 2차 묵시적 비정상적인 해석 방법이 사용되었다. 수렴 검사를 위해 허용치(tolerance)는 10-4로 설정하여 정확한 해를 얻도록 하였다.
본 연구의 성능 평가 지표로는 효율과 항력 값이 사용되었다. 효율 계산에 앞서 터빈에서 발생하는 순간 출력은 터빈의 각속도(w)와 이에 작용하는 토크(T)의 곱과 같다. 다리우스 터빈에서는 토크와 속도가 일정하지 않기 때문에 출력이 일정하지 않다. 따라서 주기 당 평균 출력은 아래와 같이 주기 당 이러한 항의 평균값의 곱으로 계산된다.
그리고 효율()은 다음과 같이 계산된다.
여기서 는 터빈의 통수 단면적으로, 2차원 모델에서는 단위 길이 높이가 사용되어 터빈 직경과 같게 된다. 는 자유 유동 속도이고 𝜌는 유체 밀도이다. 순간 항력의 경우도 출력과 유사하게 일정하지 않으므로 주기 당 평균 항력이 사용되었다.
3. 결과 및 토의
단일 터빈 수렴성 해석
먼저 단일 터빈의 출력 성능을 확인하기 위해 Fig. 5와 같은 격자 시스템을 구축하였다.
Fig. 5의 1은 전체 형상이며, 2의 터빈 회전영역은 3, 4와 같이 혼합 셀로 구성되어 있으며, 터빈 회전영역의 외부는 단일 삼각형 셀로 이루어져 있다. 터빈 회전 영역은 회전하기 때문에 슬라이드 격자를 구성하여 외부 격자와 접촉 상태를 유지하도록 하였다. 격자 수를 증가하면서 수렴성을 확인해 보았으며 3% 이내의 CP 오차를 보장하는 격자를 선택하였으며 이때 회전 영역은 338,038, 비회전 외부 영역은 135, 191 격자 수를 갖는다. 해석 시간 간격의 경우 수렴성을 확인한 후 한 주기에 200분의 1로 결정하였다. 먼저 최고 효율을 도출하는 회전속도를 구하기 위해 TSR (Tip Speed Ratio)를 변경하면서 해석을 수행하였고 그 결과 TSR 1.15에서 최고 효율을 얻을 수 있었고 이 때의 회전속도는 5 rad/sec였다.
쌍동 터빈 매개변수 해석
터빈 회전방향 효과
터빈 회전방향을 변경한 세 개 케이스에 대한 효율 검토를 수행하였으며 회전 방향은 Fig. 6에 도시하였다. 해석 조건은 단일 구성과 동일하다.
해석결과는 Table 2에 나타내었고 Case 1의 경우 단일 구성 대비 최대 50%의 효율 개선효과가 있는 것으로 확인되었다. Case 2는 Case 1의 회전 반대 방향이고 Case 3는 두 터빈이 같은 방향으로 회전하는 경우이나 모두 Case 1보다는 효율이 떨어졌다. 특히 Case2는 Case1에서 유동 방향이 180° 바뀌는 경우와 동일하므로 유향 변화에 따른 효율 차이도 예상할 수 있다.
Table 2.
Efficiencies of the single turbine and the cases of the rotational directions in the twin configuration
| Single | Case 1 | Case 2 | Case 3 | |
| CP (%) | 30 | 45 | 40 | 43 |
| Relative improvement against single (%) | 0 | 50 | 33 | 41 |
터빈 간 이격거리 효과
터빈 간 이격거리를 달리한 네 개 케이스에 대한 효율 검토를 수행하였으며 각 케이스를 아래 Fig. 7에 도시하였다.
해석 조건은 단일 구성과 동일하나 터빈 회전방향은 앞선 해석에서 가장 효율이 높았던 Case 1과 같다. 각 케이스에 대한 해석결과는 Table 3에 나열하였고 터빈 간 이격거리가 2.5R일 때 효율 향상 정도가 가장 높았으며 기존(3R)에 대비 최대 2.2%의 효율 개선 효과가 나타났다. 이는 단일 구성 대비 53% 효율 향상에 해당된다.
Table 3.
Efficiencies of the single turbine and the cases of the separation distances in the twin configuration
| 2.5R | 3R | 3.5R | 4R | |
| CP (%) | 46 | 45 | 45 | 43 |
| Relative improvement against 3R (%) | 2.2 | 0 | 0 | -4.4 |
터빈 간 이격거리와 위상차 효과
다음으로 터빈 간 이격거리와 위상차를 달리한 네 개 케이스에 대한 효율 검토를 수행하였으며 각 케이스를 아래 Fig. 8에 도시하였다. 이격거리의 경우 효율이 높은 2.5R과 3R을 선택하였고 위상차는 0°와 60°를 주어 단일 터빈과 같은 조건으로 해석해 보았다.
해석결과는 Table 4에 나열하였으며 기존 가장 높은 효율을 가졌던 조합(2.5R, 60°)인 경우, 위상차를 0°로 바꾸었더니 5%의 효율 개선효과가 나타났다. 반면(3.0R, 60°)의 경우, 위상차를 0°로 바꾸었더니 -2.6% 효율 감소효과가 나타나서 위상차와 이격거리는 상호 의존성이 있는 매개변수로 판단된다.
Table 4.
Efficiencies of the single turbine and the cases of the separation distances and the phase differences in the twin configuration
| (phase difference, separation distance) | (60°, 3R) | (0°, 3R) | (60°, 2.5R) | (0°, 2.5R) |
| CP (%) | 45 | 43.8 | 46 | 47.2 |
| Relative improvement against (60°, 3R) (%) | 0 | -2.6 | 2 | 5 |
앞의 세차례 매개변수 변화에 따른 단일 구성과 쌍동 구성의 효율을 비교한 결과, 쌍동 구성의 효율이 단일 구성에 비해 크게 효율이 향상되는 것을 확인하였다. 쌍동 구성의 경우 터빈의 회전방향, 이격거리, 그리고 위상차를 매개변수로 하여 각 케이스의 효율을 확인할 결과 쌍동 구성의 최적 형태는 터빈 간 이격거리 2.5R, 쌍동 터빈 사이에서 블레이드 이동 방향이 유동 방향과 일치, 그리고 위상차 0° 인 경우이다.
이러한 최적 구성에 대한 효율 향상의 원인을 확인하기 위해 유동 특성을 단일 구성과 비교할 수 있도록 Fig. 9에 와류와 압력 분포를 도시하였다. 하단 위치의 블레이드의 경우 쌍동 구성의 상호작용이 가장 큰 경우에 해당되어 두 구성 간 와류 및 압력 분포의 확연한 차이를 확인할 수 있다. 또한 출력에 기여하는 정도가 큰 좌상 위치의 블레이드의 경우 쌍동 구성의 압력 차가 단일 구성보다 더 크며 이는 더 큰 양력을 생성할 수 있도록 한다. 이 차이에 의해 쌍동 구성이 경우 회전력을 향상하게 되었고 상대적으로 높은 토크 및 효율을 가질 수 있는 것으로 판단된다. 유사 타 사례로서 대칭형 블레이드의 양항비(Lift-to-drag ratio)를 개선시켜 수평축 터빈의 출력을 향상시킨 선행연구(Huang et al. 2016)가 있으며 대칭형 블레이드를 주로 사용하는 다리우스 터빈에도 적용 가능한 방법이다. 이러한 양향비 개선과 본 연구에서 제시한 쌍동 구성의 장점을 동시에 활용하는 연구도 추후 가능할 것으로 판단된다.
Table 4에 나타낸 바와 같이 최적 쌍동 구성의 효율은 47.2%이며 단일 구성 대비 약 58% 증가로 상당한 효율 개선이 이루어진 바 상기 최적 형태를 쌍동 구성의 기준으로 삼아 다음 덕트 효과를 확인해 보고자 한다.
덕트 효과
대칭형 덕트의 각도에 따른 영향
먼저 덕트와 터빈 간의 이격거리를 0.5R씩 증가하면서 해석 수행하였을 때 1.5R에서 높은 효율 향상을 확인하였기에 1.5R로 고정하여 해석을 수행하였다. 효율의 경우 터빈의 통수 단면적에 대한 효율이 사용되었고 항력의 경우 터빈과 덕트의 항력을 합친 값이 사용되었다.
대칭형 덕트의 각도 10, 20, 그리고 30°에 대한 해석결과는 Table 5에 나열하였으며 출구 확산 각 30°에서 터빈 면적으로만 계산한 효율이 72.1%로 가장 높았으며 이전 최적 구성(47.2%) 대비 효율이 개선되었다. 또한 10°에서 30°로 증가하였을 때 효율은 52% 증가하였으나 항력은 156% 증가하였다. 이로 인해 구조물이 비대해지고 항력 증가도 커졌으므로 다른 방식에 대한 고려가 필요할 것으로 판단되었다.
Table 5.
Efficiencies of the difference angles in the symmetric duct
| 10° | 20° | 30° | |
| CP (%) | 47.3 | 59.2 | 72.1 |
| Drag (N/m) | 224 | 370 | 575 |
확산 덕트의 각도에 따른 영향
확산 덕트의 각도 10, 20, 그리고 30°에 대한 해석결과는 Table 6에 나열하였으며 출구 확산 각 30°에서 효율이 53%로 가장 높았으며 채널이 없는 경우(47.2%) 대비 상대적으로 효율이 향상되었다. 또한 10°에서 30°를 증가하였을 때 효율은 10% 증가하였고 항력은 22% 증가하였다. 항력의 크기 증가는 구조물의 거대화를 유발하여 비용 증가 등의 문제점이 발생하기 때문에 대칭 덕트에 비해 상대적으로 효율 향상 정도가 작지만 항력이 증가 정도가 크지 않아 확산 비대칭 덕트가 장점이 있다고 볼 수 있다.
Table 6.
Efficiencies of the difference angles in the non-symmetric duct
| 10° | 20° | 30° | |
| CP (%) | 48 | 49 | 53 |
| Drag (N/m) | 224 | 234 | 274 |
비대칭 덕트가 대칭 덕트에 비해 상대적으로 우위에 있다고 판단되나 이 경우 유향 의존성이 생기게 되어 유향이 크게 변화하는 조류 발전의 경우 유향을 맞추는 추가 기능이 요구될 수 있다는 점이 고려되어야 한다. 이에 대해서는 다음 장에 대응 방안을 제시하였다.
유향 변화 대응 방안
앞서 설명한 바와 같이 확산 비대칭 덕트의 경우 유향 의존성을 가지게 되어 원래 다리우스 터빈의 장점이 사라질 수 있다. 하천이나 인공 수로 등은 유향 변동이 크기 않은 반면 해양의 조류의 경우 반복적으로 180°로 변화하는 유향 변동성을 가지고 있다. 따라서 제시한 방식을 조류 발전에 적용하기 위해서는 유향을 맞출 수 있는 방안이 요구되며 주로 사용되는 방식은 요 제어기이다. 이는 풍력기나 수평축 조류터빈 등에 주로 사용되기는 하나 추가적인 동력 사용이 요구된다. 이에 반해 Fig. 10에 형상과 같은 제안된 가변형 덕트(고 등 2015)는 유동 에너지를 활용하여 추가적인 동력 사용 없이 유향 변화에 대응하는 해법을 제시해 줄 수 있다. Fig. 10에 표기된 바와 같이 가변형 덕트는 삼등분 되어 있고 중앙부는 레일을 따라 움직일 수 있다. 항력에 의해 밀리게 되면 롤러에 의해 피치 각이 올라가서 비대칭 형상이 되어 확산 효과를 갖게 하는 장점이 있다.
좀 더 자세히 설명하자면 먼저 흐름을 받게 되면 롤러 방식으로 기동할 수 있는 양쪽의 덕트가 항력으로 뒤로 밀리며 흐름 앞쪽의 확산기 구조는 록커(locker)에 의해 각도가 고정되며 흐름 뒤쪽에 위치한 확산기 구조는 핀에 접촉하면서 각도가 커지게 된다. 이는 반대 방향으로 흐름이 바뀌더라도 동일한 방식으로 작동하게 된다. 즉 흐름에너지를 이용한 수동 방식이나 구동기를 활용한 능동 방식을 이용하여 유향 맞춤 기능을 장착하게 되면 제안된 구성의 유체동력 터빈이 하천이나 수로 발전뿐만 아니라 조류 발전으로도 확장할 수 있을 것으로 기대된다.
4. 결 론
본 연구에서 수직축 유체동력 터빈 간 긍정적인 상호작용 효과를 통해 효율 향상을 획득할 수 있는 쌍동(twin) 터빈 방식을 채택하였고 축소 모형의 터빈에 대한 매개변수 해석을 통해 최적 구성의 형태를 도출하였다. 이어서 대칭형과 확산 효과를 활용하는 비대칭형 덕트에 대한 효율 향상 영향을 확인해 보았다. 해석 결과, 대칭형보다는 비대칭형인 확산 방식이 효율과 항력 측면에서 비교우위에 있는 것을 알 수 있었다. 다만 이로 인해 다리우스 터빈의 장점인 유향 의존성이 없는 장점이 사라지게 되어, 조류 등과 같이 방향 변동성이 큰 경우에 제안된 터빈 방식의 장점을 살리기 위한 대책이 요구될 수 있어 기존 능동 제어 방식과 더불어 추가 에너지 소모가 없는 수동 방식을 소개하였다. 본 연구에서 다룬 바와 같이 상호작용과 확산 효과를 활용하여 다리우스 터빈의 약점인 낮은 효율을 높이고, 반대 급부인 유향 의존성에 대한 영향을 최소화 하는 연구가 지속된다면 앞으로 다리우스 터빈의 활용도가 높아질 것으로 기대할 수 있다.