A New Paradigm of Artificial Neural Network Learning for Atmospheric and Oceanic Predictions: Physics-Informed Neural Networks and Operator Learning

Dong-Hoon Kim; Il-Ju Moon

doi:10.4217/OPR.2025001

Preview

Article

Ocean and Polar Research. 27 February 2025. 1-15
https://doi.org/10.4217/OPR.2025001

A New Paradigm of Artificial Neural Network Learning for Atmospheric and Oceanic Predictions: Physics-Informed Neural Networks and Operator Learning

대기 및 해양 예측을 위한 인공신경망 학습의 새로운 패러다임: 물리정보 신경망과 연산자 학습

Dong-Hoon Kim¹

Il-Ju Moon¹^*

김 동훈¹

문 일주¹^*

¹Typhoon Research Center, Jeju National University, Jeju, 63243 Korea

¹제주대학교 태풍연구센터 (63243) 제주특별자치도 제주시 제주대학교 102

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0):

This is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0), which permits unrestricted educational and non-commercial use, provided the original work is properly cited.

ABSTRACT

This study explores the potential of Physics-Informed Neural Networks (PINNs) and Operator Learning (OL) techniques in advancing scientific computation and prediction. PINNs integrate physical principles into neural network training, enabling accurate modeling and prediction of complex physical systems, even in data-scarce and noisy environments. They have been successfully applied to solve challenging nonlinear partial differential equations (PDEs), such as Euler and Navier-Stokes equations, and continue to evolve with variants. Meanwhile, OL methods, represented by Deep Operator Network (DeepONet) and Fourier Neural Operator (FNO), focus on learning mappings between function spaces. These methods excel in high-dimensional data processing and have demonstrated remarkable performance in applications such as global atmospheric modeling with NVIDIA’s FourCastNet. Hybrid approaches, such as Physics-Informed DeepONet (PIDON) and Physics-Informed Neural Operator (PINO), combine the strengths of PINNs and OL. These methods leverage data-driven learning and physical constraints, achieving superior generalization and prediction accuracy. Notably, PINO enables zero-shot super-resolution predictions by integrating multi-resolution data with PDE constraints. While PINNs and OL individually present powerful tools for modeling and prediction, their computational cost and sensitivity to noise pose challenges. Hybrid approaches offer a pathway to address these issues by optimizing their integration through quantitative analyses. Future research directions include accelerating training through high-performance computing, extending applications to multiscale problems, and designing innovative loss functions to enhance data efficiency. This work synthesizes the latest advancements in PINNs, OL, and hybrid methods, providing a new paradigm for precise and efficient scientific computation across diverse fields.

Keywords

Scientific Machine Learning (SciML)

Physics-Informed Neural Networks (PINNs)

Operator Learning (OL)

Fourier Neural Operator (FNO)

Deep Operator Network (DeepONet)

MAIN

1. 서 론
2. PINNs (물리정보 신경망) 연구 동향
PINNs의 주요 특징
PINNs의 방법론
PINNs의 연구 동향
3. OL의 연구 동향
OL과 Neural Operators
Deep Operator Network (DeepONet)
Fourier Neural Operator (FNO)
DeepONet와 FNO의 비교
4. PINNs와 OL의 결합
Physics-informed DeepONet (PIDON)
Physics-informed Neural Operator (PINO)
5. 요약 및 토론

1. 서 론

자료 의존적인(Data driven) 방법을 사용하는 기존 인공지능 모델들의 한계를 극복하기 위하여 물리정보를 기반으로 하는 신경망인 물리정보 신경망(Physics-Informed Neural Networks, PINNs)의 개발이 관심을 받고 있으며, 또 다른 방법으로 연산자 학습(Operator Learning, OL) 기술의 신속한 발전도 이루어지고 있다.

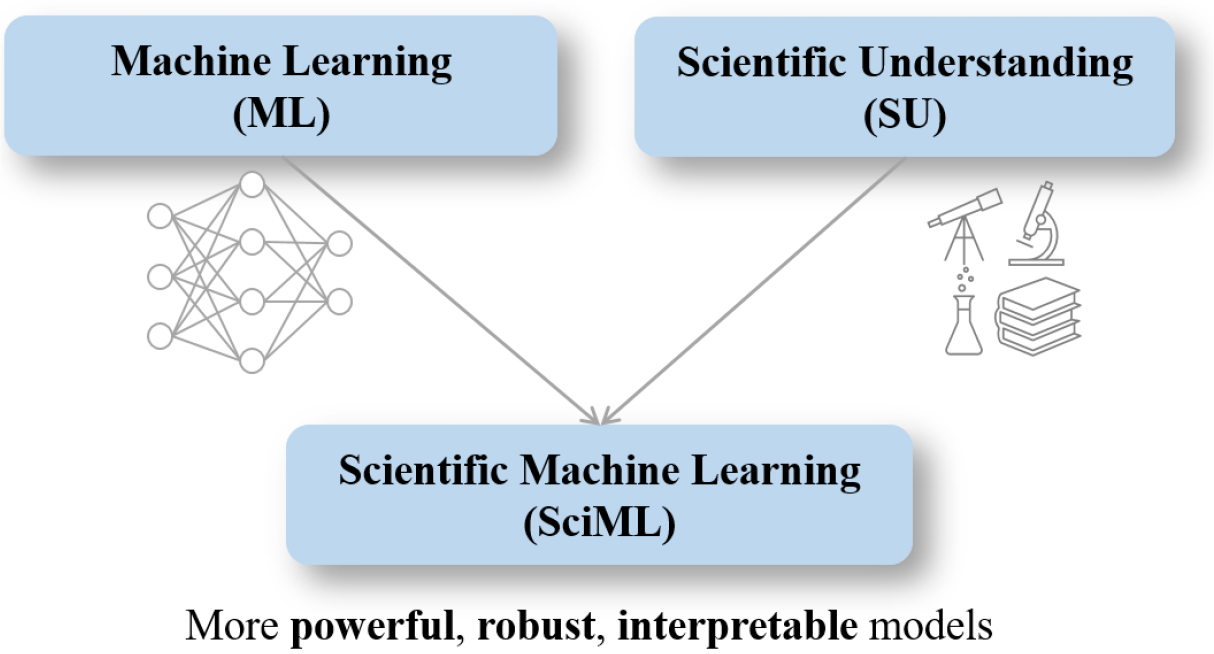
과학 연구에 기계학습(Machine Learning, ML)을 이용하기 위해 Scientific Machine Learning (SciML)이라는 용어가 생겨났다. SciML의 핵심 목표는 과학과 기계학습을 통합하는 것이다(Fig. 1). 즉, 물리법칙을 기술하는 편미분방정식(Partial Differential Equation, PDE)들을 신경망 모델에 통합하여 물리현상을 모델링하고 해석하는 것이다. 다시 말해서, SciML은 과학 연구를 위한 더욱 강력하고 견고하며 해석 가능한 방법을 생성하기 위해 기계학습과 과학 지식을 긴밀하게 결합하는 것을 목표로 한다(Baker et al. 2019).

https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F1.jpg

Fig. 1.

Conceptualization of SciML

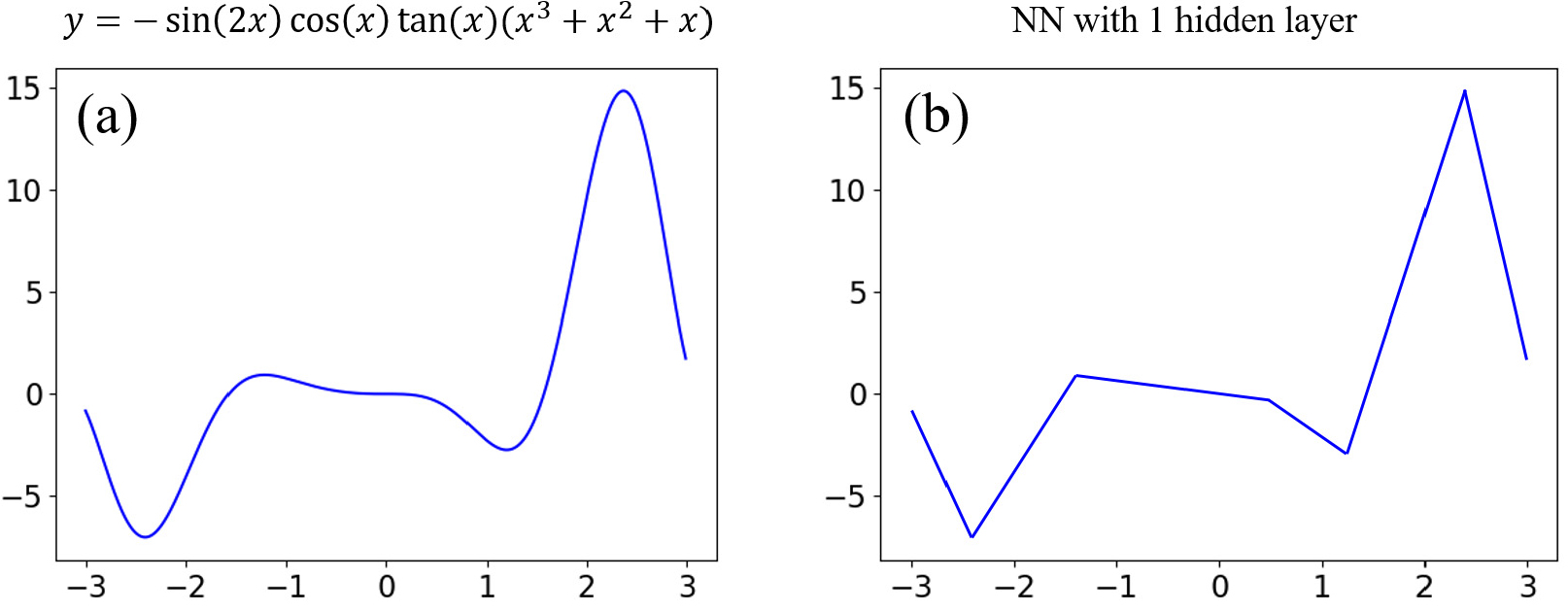
이를 위한 이론적 토대로, Cybenko (1989)는 보편근사정리(Universal Approximation Theorem, UAT)를 제시하였다. 이 정리는 어떠한 임의의 연속 함수도 단 1개의 층을 가진 순방향 신경망(Feedforward neural network)을 이용해 근사할 수 있다는 것을 보여준다 (Fig. 2). 그 후 Chen and Chen (1995)에서는 이 정리가 미분 연산자(Differential operator)에도 적용될 수 있음을 보였다. 즉, 임의의 연속 함수와 연산자를 심층 신경망(Deep Neural Network, DNN)을 이용해 근사할 수 있다는 것이다.

https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F2.jpg

Fig. 2.

Proof of the Universal Approximation Theorem (UAT). (a) A randomly generated function and its graph. (b) Shows that the function on the left can be approximated by a neural network with one layer

Cybenko (1989)는 SciML과 PINNs 구현에 있어 매우 중요한 이론적 기반을 제공한다. 실제로 Raissi et al. (2019)의 논문에서 처음으로 PINNs 모델이 제시되었고, 이후 본격적으로 물리학과 기계학습의 융합 연구가 시작되었다. Raissi et al. (2019)은 새로운 End-to-end PINNs를 제안하였고, 이를 통해 비선형(Nonlinear) PDEs를 포함하는 순방향/역방향(Forward/Inverse) 문제 모두를 효과적으로 풀 수 있음을 보였다.

SciML을 구현하기 위한 여러 방법 중에서 PINNs과 OL에 의한 기술 개발이 빠르게 이루어지고 있고, 최근에는 이 둘을 병합하여 연구하는 분야도 생겨 났다. 본 연구에서는 PINNs와 OL의 혁신적인 기술 개발 배경과 이론 및 연구 동향을 파악하여, 미래의 인공지능형 기상-해양 대순환모델 개발에 대한 전략 수립의 지침으로 삼고자 한다. 2장에서 PINNs에 대한 최근 연구동향과 3장에서 OL에 대한 최근 연구동향을 조사하였다. 4장에는 PINNs와 OL의 하이브리드(Hybrid) 결합 방법들에 대해 간략하게 소개한다. 5장에서는 요약과 토론을 제시한다.

2. PINNs (물리정보 신경망) 연구 동향

PINNs는 인공신경망의 구조를 활용하여 물리학의 원리와 법칙을 학습하고 예측하는 기술이다. 기존의 인공신경망이 주로 자료 기반(data driven)으로 학습하는 것에 비하여, PINNs는 물리학적 모델과 방정식을 신경망 학습 과정에 직접 통합한다. 이를 통해 신경망은 물리적 현상을 더 정확하게 모델링하고 예측할 수 있다. 따라서 대기 및 해양의 복잡한 물리적 현상을 모델링하는 데 특히 유용하다.

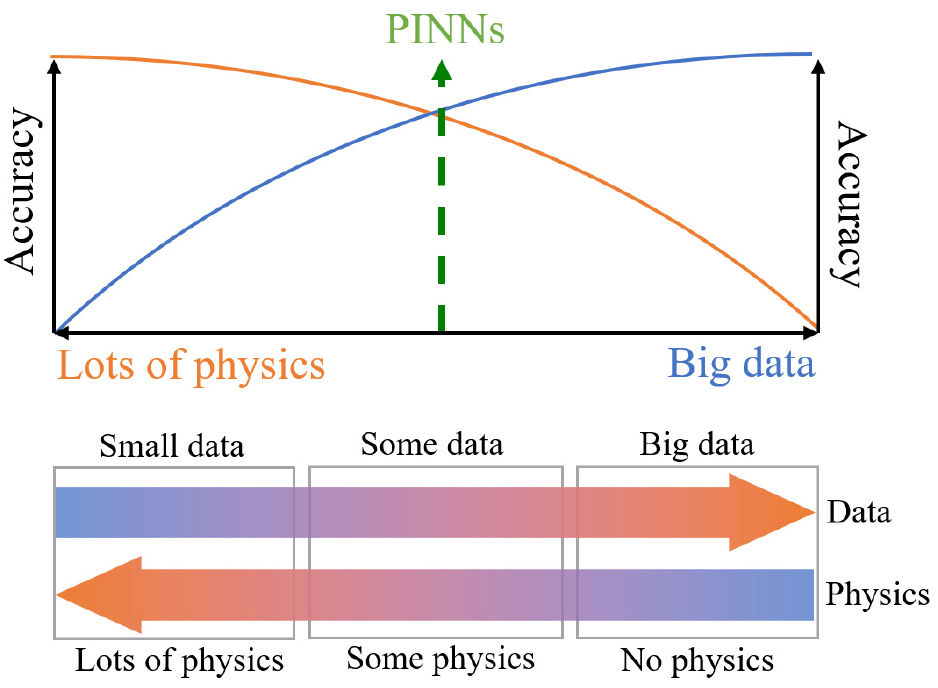
물리정보기반 신경망과 자료기반 신경망의 기여도에 따른 응용에는 세 가지의 시나리오를 생각할 수 있다(Fig. 3). 먼저, 알고 있는 물리지식이 많은 경우에는 자료가 적어도 학습 능력을 높일 수 있으며, 반대로 물리지식은 적으나 학습할 수 있는 자료가 많은 경우에도 학습 능력을 높일 수 있을 것이다. 그러나 현실에서는 물리지식도 중간 정도, 자료도 중간 정도가 있을 가능성이 높다. 이러한 시나리오에 따른 응용 분야로는 (i) 많은 물리지식을 가진 순방향 문제(Lots of physics: Forward problems) 해결, (ii) 약간의 물리지식을 가진 역방향 문제(Some physics: Inverse problems) 해결, 그리고 (iii) 물리 지식이 없는(No physics) 새로운 발견이나 시스템의 판별 등이 있다. 순방향 문제는 물리 법칙을 완전히 반영하여 제한된 자료로 복잡한 현상을 예측하는데 사용되는데, 대표적인 예로 Navier-Stokes 방정식을 기반으로 한 주변 공기 흐름 시뮬레이션을 들 수 있다. 역방향 문제는 부분적 물리지식과 자료로 미지의 매개변수를 추정하는데 사용할 수 있으며, 대표적인 예로 난류 모델의 미결정 매개변수 역산을 위하여 RANS (Reynolds-Averaged Navier-Stokes) 방정식의 폐쇄 모델(closure model)을 가정하고, 실험 자료로부터 난류 점성 계수를 학습하는 것을 들 수 있다. 물리지식이 없는 새로운 발견은 자료만으로 기존 물리 모델의 한계를 넘는 패턴을 발견하는데 사용된다. 대표적인 예로는, 해수면온도와 해양열용량 등 대규모 관측 자료를 순수 자료 기반 신경망에 학습시켜, 기존 물리 모델이 포착하지 못한 엘니뇨-남방진동의 전조 신호를 발견하는 것이다.

https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F3.jpg

Fig. 3.

Three scenarios for a physics-informed approach vs. a data-driven approach

PINNs의 주요 특징

PINNs의 핵심 아이디어는 신경망 모델의 손실 함수(Loss function)에 PDE나 다른 물리 법칙들을 제약조건으로 추가하는 것이다. 이를 통해 신경망은 자료를 학습할 뿐 아니라 주어진 물리 법칙도 만족시키도록 훈련을 받는다. 구체적으로, PINNs 모델은 다음과 같은 손실 함수를 가진다:

(1)

Loss = Data loss + PDE loss

여기서 Data loss는 실제 자료와 신경망 출력의 오차를 측정하고, PDE loss는 신경망 출력이 주어진 물리 법칙을 얼마나 잘 만족하는지 측정한다. 이는 매우 강력한 정규화(Regularization) 효과를 가져온다. 즉 자료가 부족하거나 노이즈가 많은 상황에서도, 강한 물리적 제약 조건 덕분에 훨씬 더 정확하고 일반화 성능이 높은 모델이 학습된다. 이를 통해 PINNs는 물리적 현상을 모델링하고 시뮬레이션 하는데 강력한 효과를 보인다. 특히 실험 자료가 부족한 문제에 있어서도 사전 물리적 지식 (Prior physical knowledge)을 이용해 정확한 추론을 수행할 수 있다는 장점이 있다.

접근법에 있어 Raissi et al. (2019)은 UAT (Cybenko 1989; Chen and Chen 1995)를 기반으로 사용했다. 이 정리에 의하면 임의의 함수나 편미분 연산자 (PDE Operator)는 순방향 신경망으로 근사 가능하다는 것을 보장한다. Raissi et al. (2019)은 이 정리를 바탕으로 PINNs 아키텍처를 제안했고, 이를 통해 순방향/역방향PDE 문제를 풀 수 있음을 보였다. 여기에 더해 Automatic Differentiation (AD) 기술을 접목시킴으로써, PDEs의 미분 연산들을 효율적으로 계산하고 End-to-end로 학습시킬 수 있는 토대를 마련했다.

PINNs는 물리 법칙을 모델에 직접 통합할 수 있어 해석 가능성이 높고, 소량의 자료나 잡음이 섞인 자료에서도 물리 제약조건을 통해 강건한 모델링이 가능하기 때문에 복잡한 PDE 해석, 최적화, 역문제 해결 등에 적합하고, End-to-end 딥러닝 기법을 활용하는 것이 가능하다는 장점이 있다. 그러나 PINNs는 물리 지식을 정확히 모델에 반영하기 어려울 수 있고, 복잡한 물리 시스템을 신경망으로 정확하게 근사하기 어렵기 때문에 많은 양의 자료가 있다면 기존 딥러닝 기법과 비슷한 성능을 보이고 물리방정식 구현을 위한 수치해석 지식이 필요하다는 단점이 있다. 따라서 PINNs는 복잡한 물리 시스템을 해석하는 데 한계가 있으나, 물리법칙을 잘 아는 경우에는 효과적으로 사용할 수 있다.

PINNs의 방법론

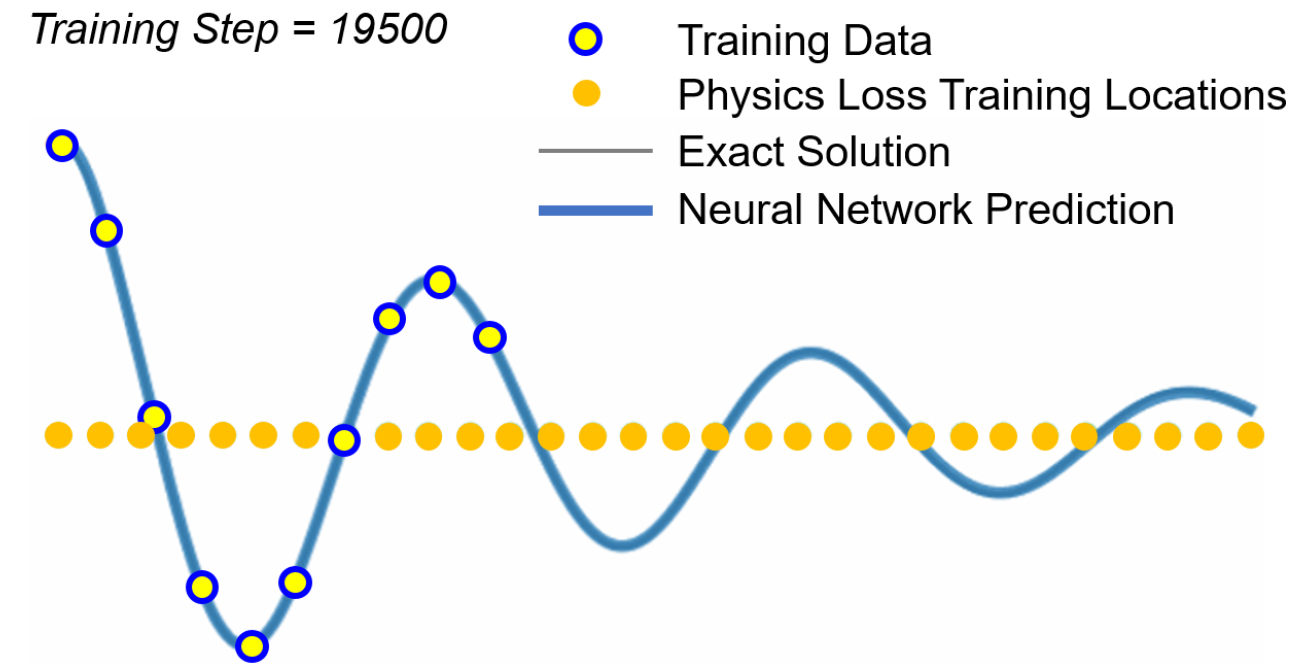
Moseley (2021)는 PINNs 방법을 잘 이해할 수 있도록 과학 연구에서 기계학습을 활용한 예를 잘 보여주고 있다. 가령, 알 수 없는 물리적 현상으로부터 일부 실험 자료가 주어졌다고 가정하자(예: Fig. 4의 주황색 점). 일반적인 과학적 과제는 이 자료를 기반으로 새로운 실험 측정값을 정확히 예측할 수 있는 모델을 찾는 것이다. 이를 기계학습을 사용하여 수행하는 한 가지 인기 있는 방법은 신경망을 사용하는 것이다. 임의의 자료의 위치를 입력으로 제공하면, 신경망은 올바른 답변을 예측하는 출력을 생성할 수 있다. 모델을 학습시키기 위해, 신경망의 자유 매개변수(θ)를 조정하여 신경망의 예측 값이 기존 실험 자료와 밀접하게 일치하도록 한다. 이는 일반적으로 예측 값과 훈련 자료 간의 평균 제곱 오차를 최소화함으로써 수행된다(Eq. 2). 그러나 이러한 모델은 알려진 실험 자료 점 내에서는 우수한 예측 성능을 발휘할 수 있지만, 자료가 없는 영역(Fig. 4에서 주황색 점이 없는 회색 우측 영역)에서는 예측 성능을 보장할 수 없다.

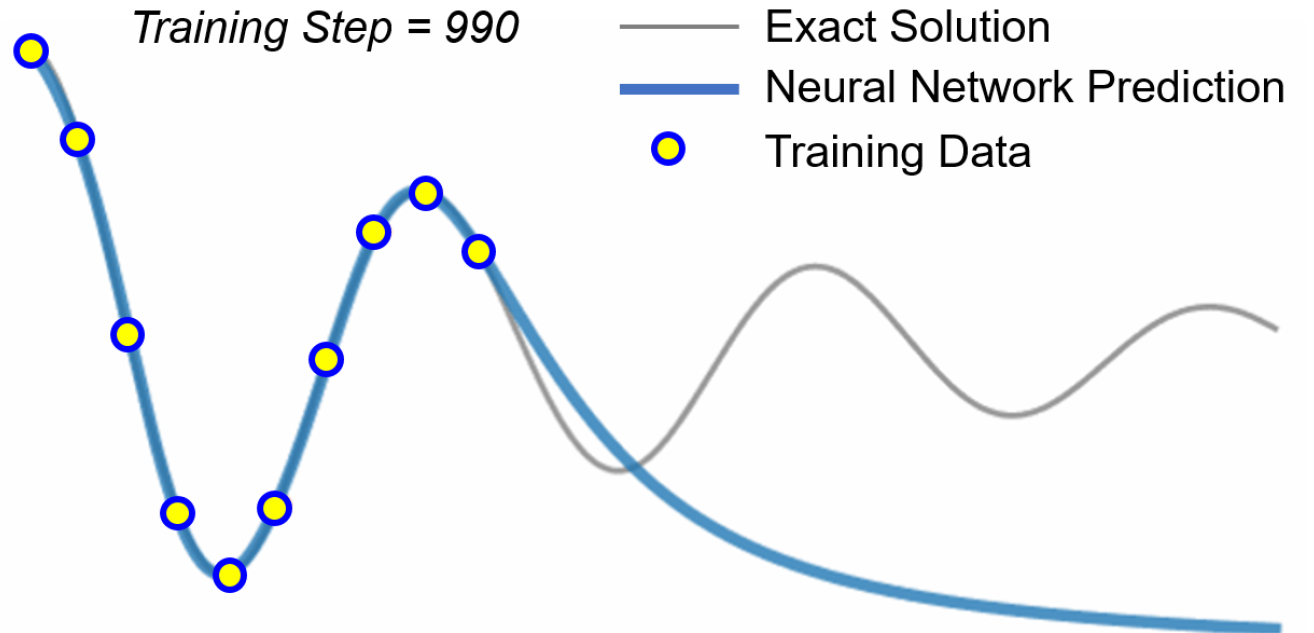
https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F4.jpg

Fig. 4.

Example of a neural network fitting a model to some experimental data.Adapted from Fig. 1 in Moseley (2021)

(2)

\min \frac{1}{N} \sum_{i}^{N} (u_{N N} (x_{i}; θ) - u_{t r u e} (x_{i}))^{2}

Fig. 4에서 정답(exact solution)으로 사용된 회색 곡선은 사실은 물리학에서 알고 있는 감쇠 고조파 방정식(Eq. 3)으로 표현된 곡선이다. 감쇠 고조파 방정식은 진동 시스템에서 감쇠와 외력이 작용하는 상황을 설명하는 미분방정식이다. 여기에서 $m$ 은 질량을 나타내며 𝜇는 마찰 계수, $k$ 는 스프링 상수이다.

(3)

m \frac{d^{2} u}{d x^{2}} + μ \frac{d u}{d x} + k u = 0

(4)

\min \frac{1}{N} \sum_{i}^{N} (u_{N N} (x_{i}; θ) - u_{t r u e} (x_{i}))^{2} + \frac{1}{M} \sum_{j}^{M} ([m \frac{d^{2}}{d x^{2}} + μ \frac{d}{d x} + k] u_{N N} (x_{j}; θ))^{2}

순수 신경망 학습에 사용된 손실함수(Eq. 2)와 여기에서 알게 된 물리정보를 합하여 새로운 손실함수(Eq. 4)로 만들어서 학습에 사용하는 것이 바로 PINNs의 방법이다. 이 손실함수를 사용하여 학습을 함으로써 관측되지 않은 범위에서의 예측 성능도 높일 수 있을 것이다. Fig. 5에서는 자료 포인트(주황색)가 없는 오른쪽 부분에도 정답인 회색과 추정치인 파란색이 잘 일치하여 회색이 보이지 않는 것을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F5.jpg

Fig. 5.

Loss functions used in physics-based neural networks. Adapted from Fig. 5 in Moseley (2021)

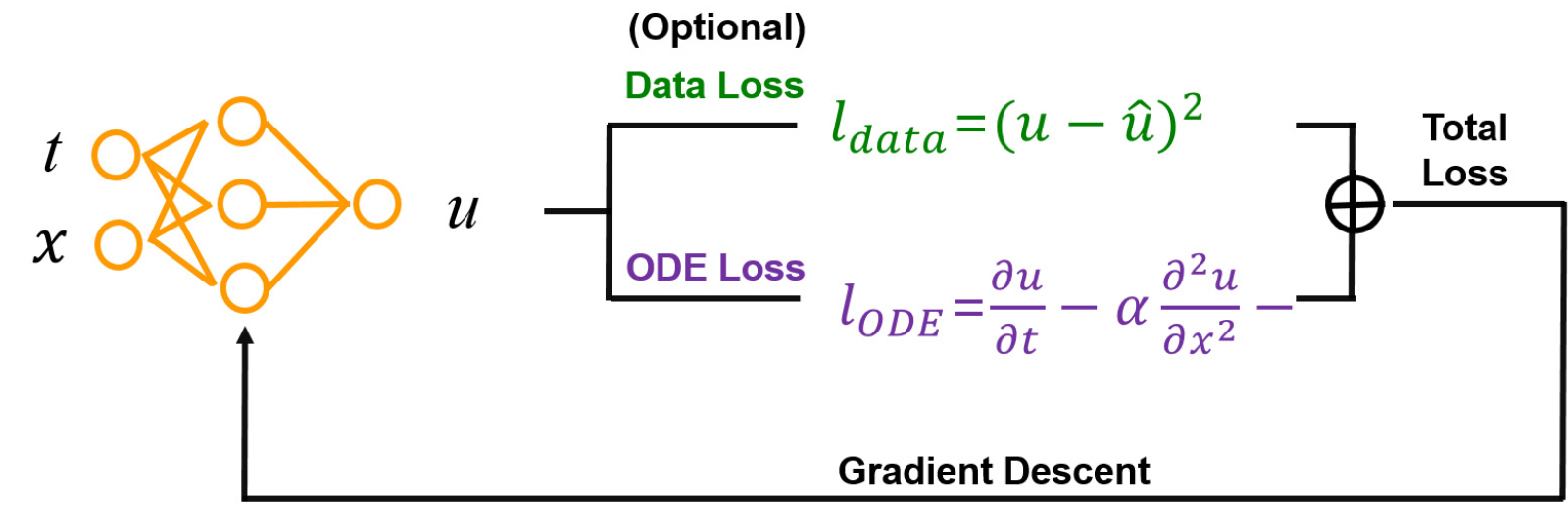
PINNs는 네트워크가 자료에만 적합하도록 훈련되는 것이 아니라 미분 방정식으로 기술된 알려진 물리 법칙을 준수하도록 훈련되는 신경망의 한 유형이다. 이는 지배 미분 방정식의 위반 정도를 측정하는 Ordinary Differential Equation (ODE)/PDE 손실을 도입함으로써 달성된다(Fig. 6). 이 방법으로, 물리 법칙을 네트워크 훈련 과정에 주입하여 물리적으로 정보를 제공하게 된다.

https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F6.jpg

Fig. 6.

The loss function of a neural network that incorporates physics information includes a contribution from the PDE loss, which is an effective measure of whether the predicted solution satisfies the governing differential equation

PINNs의 연구 동향

PINNs의 어원은 유사한 용어를 사용하는 여러 논문에서 찾을 수 있지만, Raissi et al. (2019)의 논문이 PINNs를 정확히 언급한 최초의 연구로 간주될 수 있다. 이들은 물리 법칙을 일반적인 비선형 PDE로 표현하여 이를 준수하는 동시에 지도 학습 과제를 해결하도록 학습된 신경망인 PINNs를 제안하였다. 또한 이들은 사용 가능한 자료의 성격과 배열에 따라 연속 시간 모델과 이산 시간 모델의 두 가지 알고리즘을 고안하였다. 제안된 프레임워크의 타당성은 유체역학, 양자역학, 반응-확산 시스템, 비선형 천이파 전파와 같은 고전적 문제를 통해 입증되었다.

Karniadakis et al. (2021)은 PINNs에 대한 체계적인 개요를 제공한다. 이 논문은 물리학을 기계학습 모델에 통합하는 것에 대한 포괄적인 리뷰를 제시한다. 기존 수치 해석 방법은 편미분방정식(PDE)을 이산화할 때 여러 한계를 보인다. 특히, 다양한 물리적 현상을 동시에 모델링하거나 잡음이 섞인 자료를 처리할 때, 복잡한 격자 생성, 고차원 문제 해결, 그리고 숨겨진 물리 법칙을 찾아내는 역문제(Inverse Problem)에서 어려움이 발생한다. 기계학습, 특히 딥러닝은 이러한 문제를 해결하기 위한 대안으로 부상하였으며, 일반적으로 과학적 문제 해결에 대규모 자료가 요구된다. 물리 정보 기반 기계학습은 자료를 수학적 모델과 통합하며, 신경망이나 커널 기반 회귀 네트워크를 사용하여 물리 법칙을 강제 적용한다. 이러한 모델은 향상된 정확도, 더 빠른 학습, 그리고 일반화 능력을 제공한다(Karniadakis et al. 2021). PINNs를 효율적으로 구현하기 위해서는 TensorFlow, PyTorch, Keras, JAX와 같은 최신 기계학습 라이브러리를 기반으로 새로운 알고리즘을 구축하는 것이 유리하다. 물리 기반 기계학습을 위해 특별히 설계된 여러 소프트웨어 라이브러리가 개발되었으며, 이는 이 분야의 빠른 발전에 기여하고 있다(Table 1 참조).

Table 1.

Major software libraries specifically designed for physics-informed machine learning. Adapted from Table 1 in Karniadakis et al. (2021)

Software name	Usage	Language	Backend	References
DeepXDE	Solver	Python	TensorFlow	Lu et al. (2021b)
SimNet	Solver	Python	TensorFlow	Hennigh et al. (2020)
PyDEns	Solver	Python	TensorFlow	Koryagin et al. (2019)
NeuroDiffEq	Solver	Python	PyTorch	Chen et al. (2020)
NeuralPDE	Solver	Julia	Julia	Rackauckas and Nie (2017)
SciANN	Wrapper	Python	TensorFlow	Haghighat and Juanes (2021)
ADCME	Wrapper	Julia	TensorFlow	Xu and Darve (2020)
GPyTorch	Wrapper	Python	PyTorch	Gardner et al. (2018)
NeuralTangents	Wrapper	Python	JAX	Novak et al. (2020)

Cuomo et al. (2022)은 PINNs에 관한 다양한 문헌을 포괄적으로 검토하여 PINNs와 관련된 신경망의 강점과 약점을 규명하였다. 더 나아가, 이 연구는 고전적인 PINNs를 넘어 물리적 제약 신경망(Physics-Constrained Neural Networks, PCNNs)과 변분적(Variational) hp-VPINNs, 보존(Conservation) PINNs (CPINNs)와 같은 여러 변형 신경망을 포함하고 있다. 그들은 PINNs와 관련된 대부분의 연구가 활성화 함수와 기울기 최적화 기법, 신경망 구조, 손실 함수 구조와 같은 다양한 측면을 통해 PINNs를 특화하는 데 중점을 두고 있음을 보여준다. PINNs는 유한요소법(FEM)과 같은 전통적인 수치 기법에 비해 특정 맥락에서 더 실현 가능성이 높은 잠재력을 보여주었으나, 저자들은 PINNs가 광범위한 응용 분야에 사용됨에도 불구하고 여전히 해결되지 않은 이론적 문제를 통해 발전의 여지가 남아 있다고 제안한다(Cuomo et al. 2022).

Cuomo et al. (2022)은 PINNs와 관련된 논문 수(Fig. 7의 오른쪽)와 PINNs가 적용된 문제(Fig. 7의 왼쪽)가 최근 크게 증가하고 있음을 근거로 PINNs가 문헌과 과학적 응용 모두에서 이미 상당한 영향을 미치고 있음을 보였다. 특히, 저자들은 PINNs의 대표적인 논문인 Raissi et al. (2019)를 인용하거나 제목 또는 키워드에 PINNs를 포함한 논문의 수가 기하급수적으로 증가하고 있음을 보였다. 실제로 2019년에서 2020년 사이에 PINNs 관련 논문 수는 5배 이상 증가하였으며, 2021년에는 2020년에 비해 새로운 논문 수가 두 배로 증가하였다. Raissi et al. (2019)이 2019년에 arXiv에 게재된 이후, 2018년 말과 2019년에 인용 횟수가 급격히 증가한 것을 확인할 수 있다. Fig. 7의 왼쪽에서는 해당 연도에 발표된 논문에서 해결된 특정 시간 의존 방정식의 예를 보여준다. 초기(2018년)에는 Allen–Cahn 방정식, Korteweg–de Vries 방정식, 1차원 비선형 슈뢰딩거(Shrödinger) 방정식(SE)과 같은 기본(vanilla) PINNs로 해결된 문제들이 포함되었다. 이 후, 2019년 말에 Mao et al. (2020)은 동일한 PINNs를 사용하여 고속 공기역학적 흐름을 모델링하기 위한 Euler 방정식(EE)을 해결하였다. 2020년 말에는 Jin et al. (2021)이 비압축성 Navier–Stokes 방정식(NSE)을 해결하였다. 마지막으로, 2021년에는 Cai et al. (2021)이 Navier–Stokes 방정식을 해당 온도 방정식과 결합하여 열대류 흐름(NSE+HE(Heat Eq.))을 분석하였다(Fig. 7).

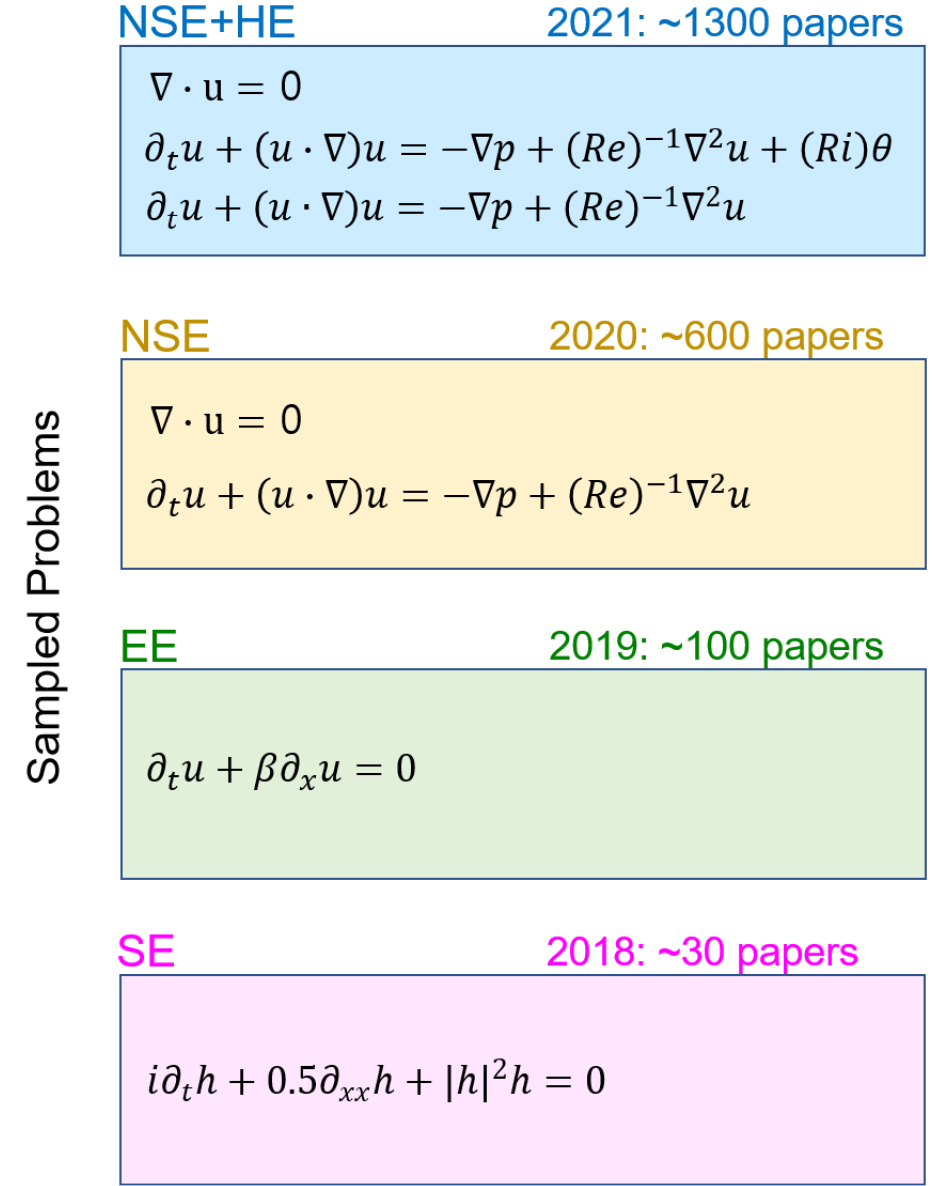
https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F7.jpg

Fig. 7.

Papers related to PINNs by year and applied problems. Here, SE, EE, NSE, and HE represent the one-dimensional Schrödinger equation, the Euler equation, the Navier-Stokes equation, and the Heat equation, respectively. Adapted from Fig. 1 in Cuomo et al. (2022)

Table 2는 PINNs의 다양한 신경망 구현을 대표하는 여러 논문을 소개한다. 여기에는 순방향 신경망(Feed-Forward Neural Networks, FFNNs), 합성곱 신경망(Convolutional Neural Networks, CNNs), 순환 신경망(Recurrent Neural Networks, RNNs)의 세 가지 주요 신경망 그룹이 포함된다. 각 유형에 대해, 해당 신경망을 처음으로 사용하거나 구현 방식을 가장 잘 설명한 논문들이 보고되었다. 이 결과에 따르면, PINNs가 주로 5~10층의 FFNN으로 구현된 것으로 나타난다. CNN은 손실 함수가 아닌 신경망 구조에 경계 조건을 통합하는 Physics-Constrained Neural Network (PCNN) 접근법에서 처음으로 적용되었다(Cuomo et al. 2022).

Table 2.

References representing different neural network implementations of PINNs. Adapted from Table 1 in Cuomo et al. (2022). Here, FF-NN, FC-DNN, AE, LSTM, BNN, and GAN represent Feed-Forward Neural Network, Fully Connected Deep Neural Network, Autoencoder, Long Short-Term Memory, Binarized Neural Network, and Generative Adversarial Network

NN family	NN type	References
FF-NN	1 layer/EML	Dwivedi and Srinivasan (2020), Schiassi et al. (2021)
	2–4 layers	32 neurons per layer He et al. (2020), 50 neurons per layer Tartakovsky et al. (2020)
	5–8 layers	250 neurons per layer Zhu et al. (2021)
	9+ layers	Cheng and Zhang (2021), Waheed et al. (2021)
	Sparse	Ramabathiran and Ramachandran (2021)
	multi FC-DNN	Amini Niaki et al. (2021), Islam et al. (2021)
CNN	plain CNN	Gao et al. (2021), Fang (2021)
CNN	AE CNN	Zhu et al. (2019), Geneva and Zabaras (2020), Wang et al. (2021a)
RNN	RNN	Viana et al. (2021)
RNN	LSTM	Zhang et al. (2020), Yucesan and Viana (2021)
Other	BNN	Yang et al. (2021)
Other	GAN	Yang et al. (2020)

3. OL의 연구 동향

최근 인공신경망 연구에서 OL은 PINNs와 함께 주목받고 있는 분야이다. 이 분야는 주로 심층 연산자 네트워크(Deep Operator Network, DeepONet)과 푸리에 신경 연산자(Fourier Neural Operator, FNO)라는 두 가지 주요 방법론으로 나뉜다. 이들은 복잡한 물리 시스템이나 프로세스를 모델링하는 데 사용되며, PINNs와 마찬가지로 물리학과 딥러닝의 융합을 시도한다(Choi et al. 2024).

PINNs는 많은 응용 분야에서 효과적임이 입증되었지만, 몇 가지 한계점도 존재한다. PINNs는 특정 입력 매개변수(예: 경계 및 초기 조건, 외부 강제력 등)에 대해 학습되며, 입력 매개변수가 변경될 때마다 PINNs를 다시 학습시켜야 한다. 따라서 다양한 작동 조건에서 실시간 추론을 수행하는 데는 효율적이지 않다. 반면, 연산자를 직접 학습하는 접근법은 서로 다른 조건에서 추론을 가능하게 하는 이점을 제공한다. 연산자 학습(OL) 기술은 대기 및 해양 자료의 복잡한 패턴을 학습하여 기상-기후 모델링 및 예측의 정확성을 높이는 데 기여할 수 있다.

이 절에서는 OL의 일종인 함수 공간 간의 매핑(Mapping)을 학습하고 편미분 방정식을 해결하는 모델인 신경 연산자(Neural Operators)를 소개한다. Neural Operators에 대한 보다 상세한 정보는 Li et al. (2021, 2023)과 Kovachki et al. (2023), Serrano et al. (2023) 등의 연구에서 확인할 수 있다. Neural Operators의 실제 구현 및 응용은 다양한 방법을 통해 진행되고 있으며, 본 절에서는 특히 주목받고 있는 두 가지 접근법인 DeepONet과 FNO에 대해 상세히 설명한다.

OL과 Neural Operators

OL은 주어진 입력 함수나 자료를 기반으로 출력을 생성하는 연산자를 학습하는 방법이다. 즉, 입력과 출력 간의 복잡한 관계를 모델링하는 데 중점을 둔다. 이러한 연산자는 물리적 시스템, 화학 반응, 날씨 변화 등 다양한 분야의 동적 시스템에 적용된다. 특히, 신경망을 사용하여 OL을 시도하는 특정 방법을 Neural Operators라고 한다. Neural Operators는 입력 함수에서 출력 함수로의 매핑을 신경망을 통해 학습한다. Neural Operators는 주로 합성곱 신경망(CNNs) 또는 그래프 신경망(GNNs)과 같은 딥러닝 구조를 사용한다. 이러한 네트워크는 함수의 특성을 학습하고 복잡한 연산자를 효율적으로 근사할 수 있다.

Neural Operators의 주요 특징을 정리하면 다음과 같다: (i) 전통적인 기계학습 모델은 스칼라 또는 벡터 입력을 처리하는 반면, Neural Operators는 함수 자체를 입력과 출력으로 처리한다. 이는 연속 자료나 고차원 공간에서의 문제를 모델링하는 데 적합하다. (ii) Neural Operators는 많은 과학 및 공학 분야에서 중요한 PDE을 해결하는 역할을 한다. 이는 계산수학, 유체역학, 물리학 등 다양한 분야에 적용될 수 있다. (iii) Neural Operators는 특정 PDE의 해를 학습하는 것이 아니라, 다양한 조건과 매개변수를 가진 여러 유형의 PDE에 대한 일반적인 해법을 학습할 수 있다. 예를 들어, 한 번 훈련된 모델로 열확산 방정식과 Navier-Stokes 방정식을 모두 해결할 수 있다. 이는 학습 과정에서 접해보지 못한 새로운 조건이나 매개변수를 가진 PDE에 대해서도 효과적인 예측을 수행할 수 있음을 의미한다. (iv) Neural Operators는 대규모 자료셋과 고성능 컴퓨팅 자원을 활용하여 학습된다. 이는 대규모 시뮬레이션 자료를 요구하는 과학 및 공학 연구에서 특히 중요하다. (v) Neural Operators는 종종 딥러닝 신경망 구조를 활용하여 복잡한 함수 매핑을 효율적으로 학습한다.

Deep Operator Network (DeepONet)

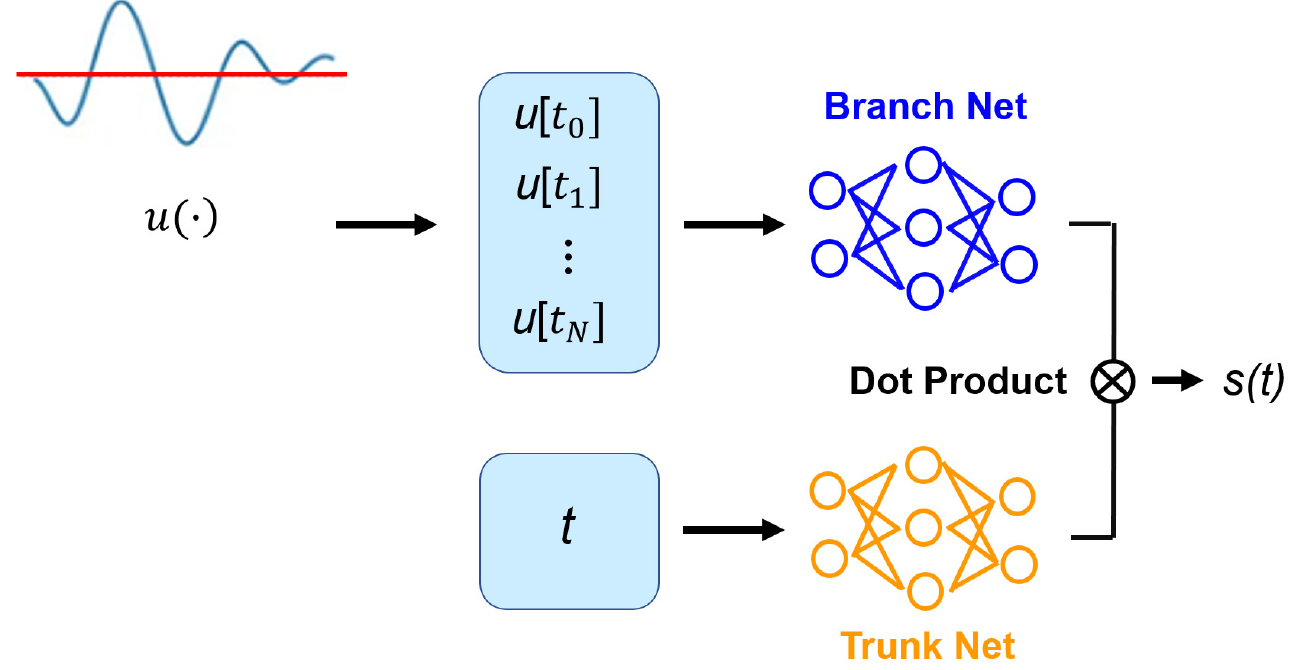
DeepONet은 Neural Operator의 한 형태로(Lu et al. 2021a) 함수 간의 복잡한 관계를 학습하는 데 중점을 둔다. DeepONet은 입력 함수 u(⋅)를 처리하는 브랜치(Branch) 네트워크와 시･공간 좌표를 처리하는 트렁크(Trunk) 네트워크로 구성된다(Fig. 8). 두 네트워크의 출력은 동일한 차원을 가지며, 이를 내적(dot product)을 통해 병합한다. 선택적으로, 내적 이후에 편향(bias) 항을 추가하여 모델의 표현력을 더욱 향상시킬 수 있다(Guo 2023).

DeepONet은 다양한 유형의 함수와 연산자에서 효과적으로 작동하며, 학습된 연산자는 새로운 또는 미지의 입력 함수에도 일반화가 잘 된다. 이 모델은 유체역학, 재료과학, 기상학, 생물 시스템 모델링과 같은 다양한 분야에 적용된다. 특히 복잡한 PDE를 해결하거나 고차원 자료를 처리하는 데 유용하다. DeepONet은 특히 시간에 따라 변화하는 프로세스나 공간적으로 분포된 현상을 모델링하는 데 적합하다.

https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F8.jpg

Fig. 8.

The structure of DeepONet. Adapted from Fig. 7 in Guo (2023)

DeepONet은 전통적인 수치 기법에 비해 낮은 계산 비용으로 복잡한 연산자를 효율적으로 근사할 수 있을 뿐 아니라 학습이 완료된 후에는 다양한 유형의 입력에 대해 정확한 예측을 제공할 수 있다. DeepONet은 또한 실험 자료나 시뮬레이션 자료를 기반으로 학습할 수 있어, 물리적 모델이 명확하지 않은 경우에도 유용하다. 즉, DeepONet은 딥러닝과 수치 해석을 결합한 혁신적인 접근법이며, 복잡한 시스템을 모델링하고 예측하는 데 새로운 방향을 제시한다(Lu et al. 2021a).

Fourier Neural Operator (FNO)

FNO는 연산자를 학습하기 위해 푸리에 변환을 기반으로 한다. 푸리에 변환은 함수를 시간 또는 공간 영역에서 주파수 영역으로 변환하여 복잡한 함수를 단순한 주파수 성분으로 분해한다. FNO는 푸리에 변환을 활용하여 고차원 자료를 효율적으로 처리할 수 있으며, 복잡한 PDE를 해결하는 데 높은 정확도를 보여준다. 특히, FNO는 입력 함수를 푸리에 공간으로 변환한 뒤, 이 공간에서 학습을 수행하기 하기 때문에 전통적인 신경망과 달리, 공간적 또는 시간적 연속성에 기반한 특징을 효과적으로 학습할 수 있게 한다. 따라서 FNO는 파동 방정식, 난류, 그리고 기타 복잡한 물리 시스템을 모델링하는 데 특히 효과적이다(Choi et al. 2024).

고전적인 신경망 개발은 주로 유한 차원의 유클리드 공간(Euclidean Space) 간 매핑을 학습하는 데 초점을 맞췄다. 최근에는 이를 함수 공간 간 매핑을 학습하는 Neural Operators로 일반화하였다. PDE의 경우, Neural Operators는 특정 함수 매개변수 의존성으로부터 해(Solution)로의 매핑을 직접 학습한다. 따라서, 전통적인 방법이 방정식의 하나의 사례를 해결하는 것과 달리, 신경 연산자는 PDE 전체를 학습한다.

FNO에서는 푸리에 공간에서 적분 커널을 직접 매개변수화하여 표현력 있고 효율적인 구조를 가진 새로운 신경 연산자가 제안되었다. Li et al. (2021)은 FNO를 사용하여 Burgers 방정식, Darcy 흐름, 그리고 Navier-Stokes 방정식에 대한 실험을 수행하였다. 여기서 사용된 FNO는 제로샷 초고해상도(zero-shot super-resolution) 방식으로 난류 흐름을 성공적으로 모델링한 최초의 기계학습 기반 방법이다. 이는 전통적인 PDE 해석기보다 최대 세 배 속도가 빠르며, 고정된 해상도에서 이전의 학습 기반 해석기보다 우수한 정확도를 달성한다.

FNO는 이렇게 푸리에 변환을 기반으로 하기 때문에 고차원 PDE를 해결하는 데 있어 빠른 계산 속도와 높은 정확도를 제공하며 학습된 모델은 다양한 입력 조건에 대해 잘 일반화할 수 있다는 장점이 있지만 특정 유형의 비선형 문제나 극한 조건에서는 성능이 제한될 수 있다는 단점이 있다.

Fig. 9는 신경 연산자의 전체 구조(a)와 푸리에 층(b)을 설명한다(Li et al. 2021). 신경 연산자의 전체 구조에서 입력 a(x)는 신경망 P에 의해 고차원 채널 공간으로 승격된다. 이후, 네 개의 적분 연산자 층과 활성화 함수가 적용된다. 마지막으로, 신경망 Q가 대상 차원으로 다시 투영하여 u(x)를 출력한다. 푸리에 층(b)에서는 입력 v(x)로 시작하여 상단에서 푸리에 변환 F가 적용된다. 푸리에 주요 모드에는 선형 변환 R이 적용되며, 나머지 모드들은 필터링된다. 이후, 역푸리에 변환 F^-1이 적용된다. 하단에서는 지역적 선형 변환 W가 적용되며 R에서 처리하지 못한 단기모드를 포함하여 학습하게 된다.

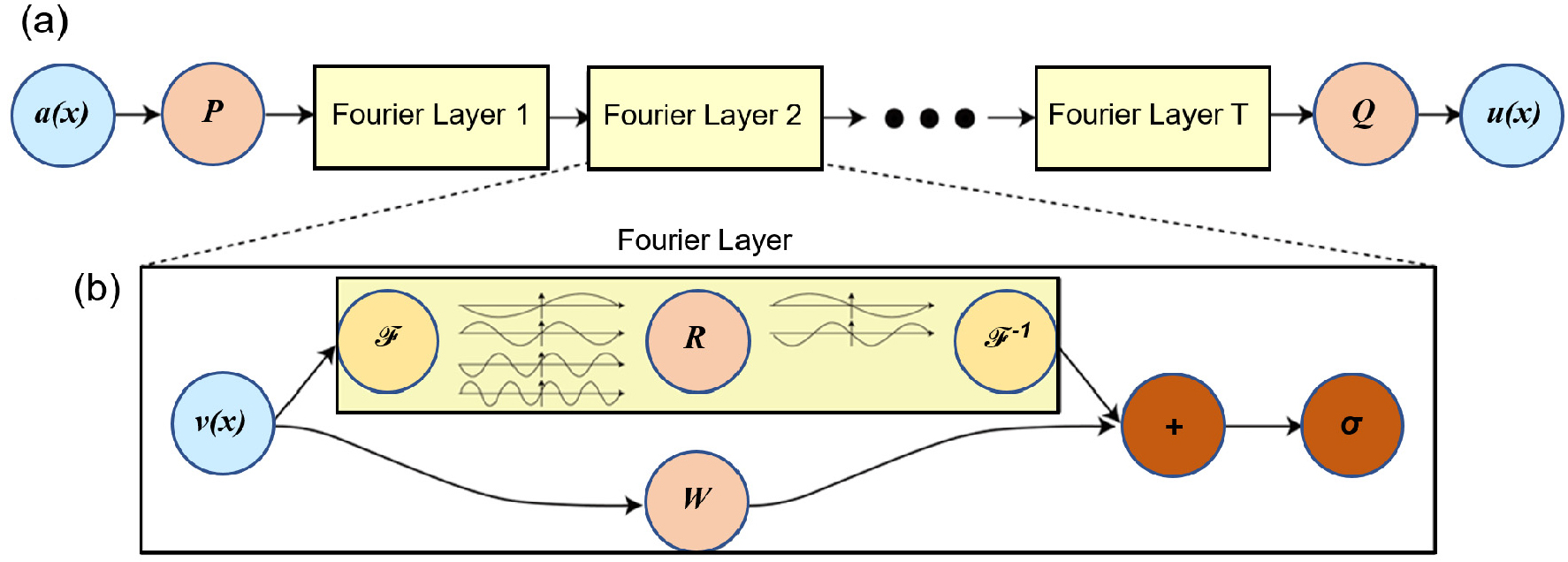
https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F9.jpg

Fig. 9.

Learning Operator. (a) The full architecture of neural operator, (b) Fourier layers. Adapted from Fig. 2 in Li et al. (2021)

FNO는 2022년 기상학 분야에서 AI 기반 전지구 대기 순환 모델에 적용되었다(Pathak et al. 2022). 이 연구에서는 AFNO (Adaptive Fourier Neural Operator)를 개발하여 FourCastNet 모델을 구축하였으며, 이는 유럽중기예보센터(European Centre for Medium-Range Weather Forecasts, ECMWF)의 수치모델 기반 통합예보시스템(Integrated Forecast System, IFS)과 유사한 성능을 달성하였다. 이후, 이 모델은 극지방의 좌표계 문제를 해결하기 위해 SFNO (Spherical Fourier Neural Operator)가 적용되어 FourCastNet의 개선된 버전으로 이어졌다(Bonev et al. 2023). Fig. 10은 ECMWF의 IFS 결과와 SFNO의 성능 비교를 보여준다.

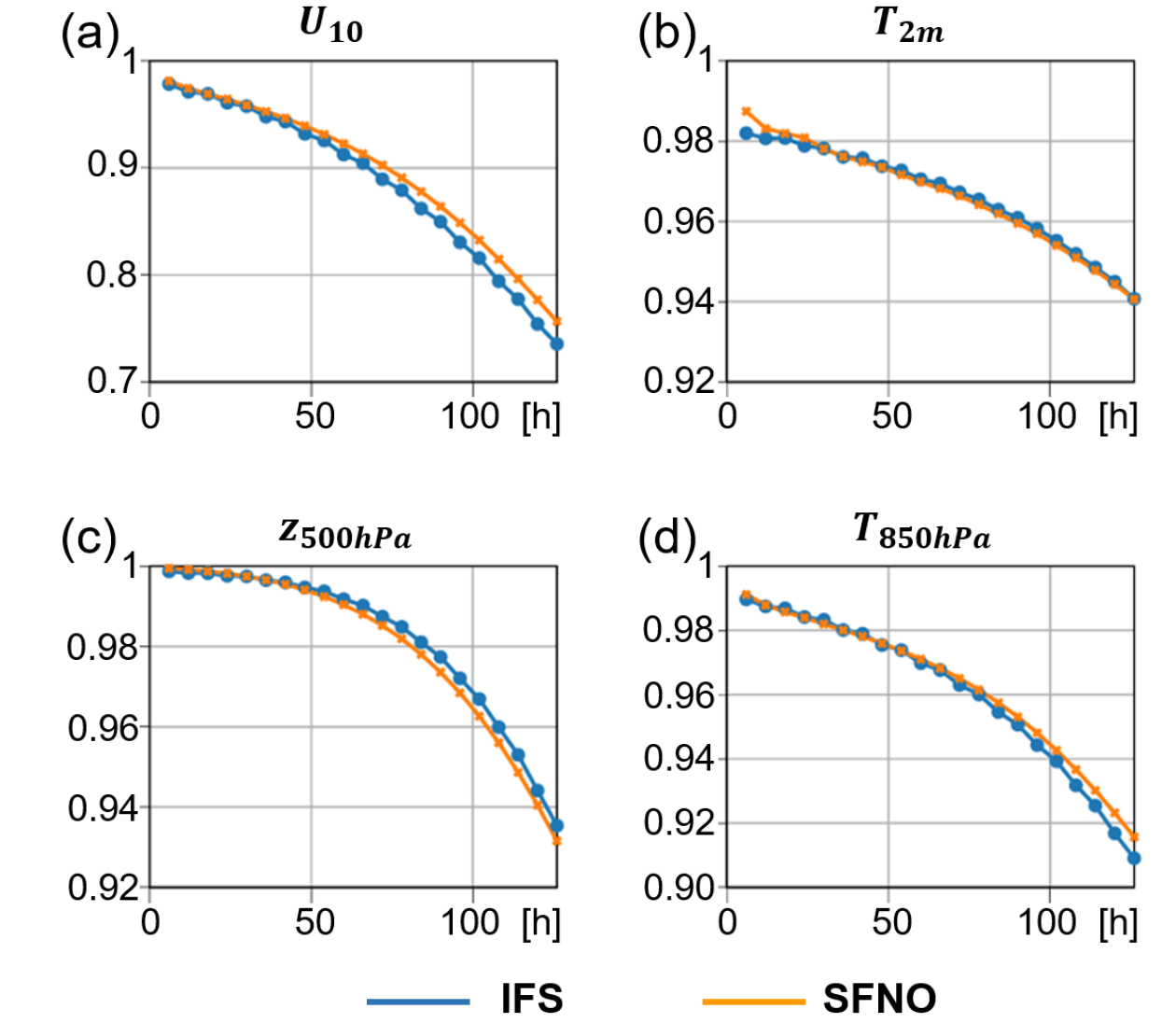
https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F10.jpg

Fig. 10.

Comparison of forecast skill (accuracy score, i.e., probability of a correct decision) as a function of prediction lead time (in hours) between IFS (blue) and the SFNO (orange) for four physical variables. (a) u₁₀ (surface wind at latitude); (b) T_2m (temperature 2 meters above the surface); (c) z_500hPa (geopotential height at 500 hPa); (d) T_850hPa (temperature at 850 hPa). Adapted from Fig. 6 in Bonev et al. (2023)

DeepONet와 FNO의 비교

Lu et al. (2022)는 FAIR (Findability, Accessibility, Interoperability, and Reusability) (Wilkinson et al. 2016) 자료를 기반으로 실용적 확장 측면에서 두 가지 Neural Operator (DeepONet와 FNO)에 대한 종합적인 비교를 연구하였다. Neural Operator는 함수 공간 간의 비선형 매핑을 학습할 수 있으며, 과학 및 공학 분야에서의 시스템 식별뿐만 아니라 다양한 응용 분야에서 복잡한 동역학의 실시간 예측을 위한 새로운 시뮬레이션 패러다임을 제공한다. 이 연구에서는 두가지 Neural Operators의 성능을 조사하고, 이를 더욱 정확하고 견고하게 만들기 위해 새로운 실용적 확장을 개발하였다. 특히, 복잡한 산업적 응용에 더욱 적합하도록 개선되었다. 첫 번째 Neural Operator인 DeepONet (Lu et al. 2021a)은 2019년에 발표되었고, 두 번째인 FNO (Li et al. 2021)는 2020년에 발표되었다. 이후에 FNO와 DeepONet를 실제 환경에서 적용하기 위해, 입력 및 출력 함수 공간의 차원이 서로 다른 매핑과 복잡한 기하학적 영역을 처리할 수 있는 FNO의 여러 확장 모델이 개발되었고 DeepONet에 유도된 편향(induced bias)을 추가하여 학습을 가속화할 수 있고 FNO와 유사한 계산 비용으로 작동하는 DeepONet의 확장 모델들이 제시되었다(Lu et al. 2022).

DeepONet과 FNO의 성능은 비교적 단순한 환경에서는 유사하지만, FNO는 복잡한 기하학적 구조나 특히 노이즈가 있는 자료에서 성능이 크게 저하된다. 예를 들어, 불안정 파동 분석에서 입력 자료에 0.1%의 노이즈만 추가해도 FNO의 오류는 10,000배 증가하여 중요한 응용에 부적합한 반면, DeepONet은 이러한 노이즈의 영향을 크게 받지 않는다. 또한, 두 Neural Operators를 이론적으로 비교했을 때 동일한 정규분포 가정 하에서는 DeepONet과 FNO 모두에서 유사한 오류 추정치를 얻을 수 있다. 그러나, Lu et al. (2022)는 Burgers 방정식과 Navier-Stokes 방정식을 사용하여 DeepONet과 FNO의 성능을 비교한 결과, DeepONet이 FNO보다 우수한 성능을 보여주었다.

4. PINNs와 OL의 결합

PINNs는 물리적 법칙을 신경망 학습 과정에 통합함으로써 모델이 물리적으로 타당한 예측을 생성하도록 보장한다. 따라서 자료가 제한적인 경우에도, 물리적 법칙을 사용하여 학습하기 때문에 효과적이며 물리적 법칙이 모델에 내장되어 있어 결과의 해석 가능성이 높다. 그러나, 물리적 법칙을 신경망에 통합하는 것은 종종 계산적으로 복잡하고 학습 시간이 길어질 수 있을 뿐 아니라 특정 물리적 법칙에 맞춰진 모델은 다른 유형의 문제에 적용하기 어려울 수 있다.

OL은 다양한 종류의 문제에 적용할 수 있는 범용적인 연산자 학습 능력을 가진다. 특히 DeepONet이나 FNO와 같은 방법은 복잡한 시스템을 빠르고 효율적으로 모델링할 수 있다. 다양한 유형의 함수 매핑을 학습할 수 있어, 복잡한 PDE와 같은 문제에 유용하다. 그러나, OL은 물리적 법칙을 직접적으로 통합하지 않아, 물리적으로 비현실적인 결과를 예측할 수 있을 뿐 아니라 정확한 학습을 위해서는 충분하고 대표적인 학습 자료가 필요하다.

이렇게 PINNs와 OL은 모두 복잡한 시스템을 모델링하고 예측하기 위한 딥러닝 기반의 방법론이지만, 각각의 접근 방식과 적용 범위에서 장단점을 가진다. 최근에는 PINNs와 OL의 장단점을 고려하여 둘을 결합한 하이브리드 방법들인 Physics-informed DeepONet (PIDON)과 Physics-Informed Neural Operator (PINO)이 개발되었다.

Physics-informed DeepONet (PIDON)

PIDON의 주요 원리는 DeepONet과 PINNs의 장점을 결합하는 것이다. DeepONet과 마찬가지로 PIDON은 함수를 입력으로 받고 함수를 출력으로 생성할 수 있다. 이는 새로운 입력 함수에 대해 재학습 없이 실시간 추론을 수행하는 데 매우 효율적이다. PIDON은 PINNs와 유사하게, 모델의 예측이 알려진 미분 방정식에 얼마나 잘 부합하는지를 측정하기 위해 손실 항을 추가한다. 이 손실 함수를 최적화함으로써, 모델은 자료 일관성(훈련 중 측정 자료가 제공되는 경우)과 물리적 일관성(Fig. 11에 제시된 바와 같이)을 모두 갖춘 예측을 학습한다. PIDON은 두 접근법의 강점을 결합한 강력한 도구이다(Wang et al. 2021b; Guo 2023).

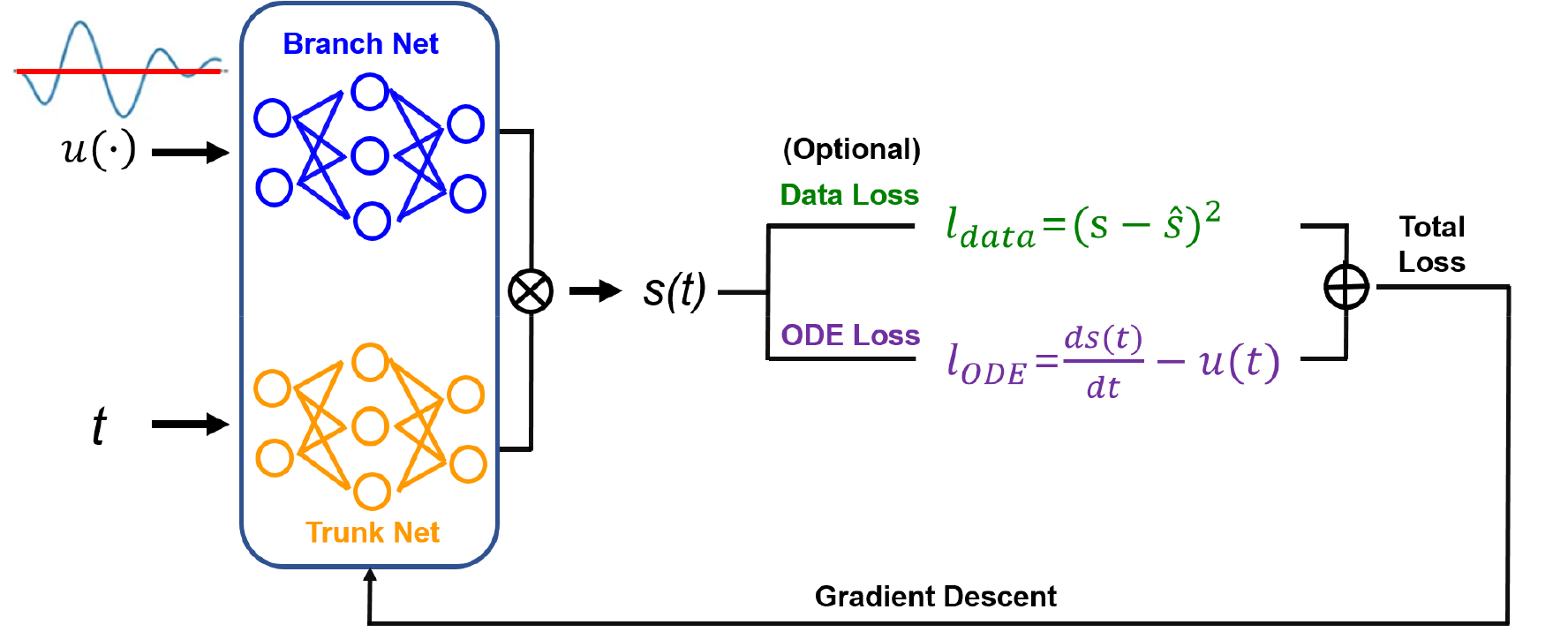
https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F11.jpg

Fig. 11.

Physics-informed DeepONet uses DeepONet as the backbone architecture while leveraging the concept of physics-informed learning to train the model. Adapted from Fig. 10. in Guo (2023)

Physics-informed Neural Operator (PINO)

Li et al. (2023)은 주어진 매개변수화된 PDE에 대한 해 연산자를 학습하기 위해 훈련 자료와 물리적 제약을 결합한 PINO를 제안하였다. PINO는 자료와 PDE 제약을 서로 다른 해상도에서 통합하여 연산자를 학습하는 최초의 하이브리드 접근법이다. 구체적으로, PINO는 저해상도의 훈련 자료를 더 높은 해상도에서 적용된 PDE 제약과 결합한다. 이렇게 개발된 PINO 모델은 많은 대표적인 PDE 계열에 대해 실제 해 연산자를 정확히 근사할 수 있으며, 훈련 자료의 해상도를 초과한 영역에서도 예측할 수 있는 제로샷 초고해상도(zero-shot super-resolution)에서 정확도를 유지한다.

PINO는 FNO 프레임워크를 사용하며, 이는 모든 연속 연산자에 대한 보편적 근사자로 작동하고, 메시(Mesh) 형태로 세분된 환경에서도 이산화 수렴을 보장한다. 이 방법은 FNO에 PDE 제약을 더 높은 해상도로 통합함으로써, 실제 연산자의 고신뢰도 재구성을 달성할 수 있다. 더욱이, PINO는 훈련 자료가 전혀 없고 오직 PDE 제약만 존재하는 조건에서도 적용이 가능하다. 이러한 결과는 Kolmogorov 흐름과 같은 다중 스케일 동적 시스템에서 최적화 문제로 실패하는 PINNs와는 대조적인 성과를 보여준다(Li et al. 2023).

Fig. 12는 학습 손실 함수와 PDE 손실 함수를 함께 사용하여 신경 연산자를 학습하는 PINO의 한 예를 보여준다. 특히, 여기서 입력 함수 a를 받아 더 큰 공차를 가진 함수 v₀를 출력하는 점별(point-wise) 승격 연산자가 포함된 신경 연산자 구조를 잘 보여준다. 이 연산 뒤에는 비선형성을 따르는 선형 적분 연산자를 계산하는 L개의 블록이 이어지며, 마지막 층은 함수 v_L을 출력한다. 점별 투영 연산자는 v_L을 투영하여 출력 함수 u를 생성한다. v_L과 u는 모두 함수이며, 이들의 모든 도함수(Dv_L, Du)는 임의의 질의점 x에서 정확한 형태로 계산될 수 있다.

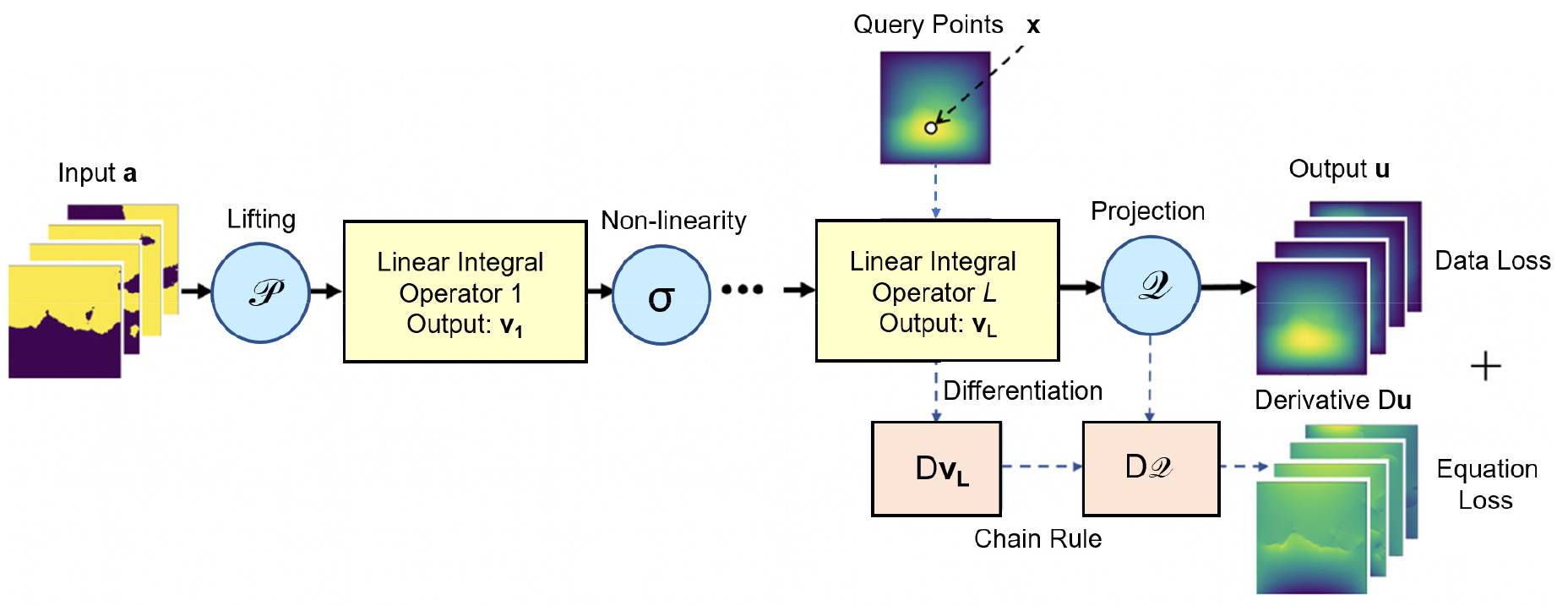
https://cdn.apub.kr/journalsite/sites/opr/2025-047-00/N00804701/images/opr_47_01_F12.jpg

Fig. 12.

PINO trains neural operator with both training data and PDE loss function. Adapted from Fig. 2 in Li et al. (2023)

5. 요약 및 토론

본 연구는 물리정보 신경망(PINNs)과 연산자 학습(OL) 기술을 중심으로 과학적 계산 및 예측의 새로운 가능성을 조사하였다. PINNs는 물리학적 원리를 신경망 학습 과정에 통합하여 복잡한 물리적 시스템의 모델링과 예측을 가능하게 하며, OL은 함수 공간 간의 매핑을 학습하여 다양한 입력 조건에서 효율적이고 확장 가능한 추론을 수행한다. 본 연구는 두 기술의 이론적 기반, 최근 연구 동향, 그리고 이를 결합한 하이브리드 접근법에 대해 논의하였다.

PINNs는 UAT을 기반으로 물리적 법칙을 신경망 학습의 손실 함수에 포함함으로써 자료가 부족하거나 잡음이 많은 환경에서도 높은 일반화 성능을 달성할 수 있다. 특히, 이 기술은 복잡한 비선형 PDE의 해법으로 확장되었으며, Euler 방정식, Navier-Stokes 방정식 등 다양한 문제를 해결하는 데 활용되고 있다. 최근에는 cPINNs, vPINNs, hp-VPINNs 등으로 발전하며 응용 범위를 확대하고 있다.

OL은 PINNs와 함께 주목받는 분야로, 함수 공간 간의 매핑을 학습하는 DeepONet와 FNO가 대표적인 기법이다. DeepONet은 함수 간의 복잡한 관계를 학습하여 다양한 유형의 PDE 문제를 효과적으로 해결할 수 있으며, FNO는 푸리에 변환을 기반으로 고차원 자료를 효율적으로 처리할 수 있다. 특히, NVIDIA의 FourCastNet은 FNO를 활용하여 기후 예측 모델을 구축함으로써 전통적 수치 모델과 유사한 성능을 입증하였다.

PINNs는 물리 법칙을 직접 신경망에 통합하여 복잡한 기상 현상이나 해양 순환을 모델링하는 데 효과적이다. 이는 불완전한 관측 자료를 보완하고 물리적으로 일관된 예측을 제공할 수 있다. OL은 위성 이미지나 시계열 자료와 같은 다양한 입력을 처리할 수 있어, 태풍 강도 예측이나 해수면 온도 변화와 같은 복잡한 기상-해양 현상을 모델링하는 데 유용하다. 특히 실시간 예측이 가능해 극단적 기상 현상에 대한 신속한 대응에 도움을 줄 수 있다. 하이브리드 접근법으로 제안된 PIDON과 PINO는 이러한 PINNs와 OL의 장점을 결합한 모델로, 자료 기반 학습과 물리적 제약을 통합하여 더 높은 예측 성능과 일반화 능력을 제공한다. 특히, PINO는 다양한 해상도의 자료와 PDE 제약을 통합하여 제로샷 초고해상도(Zero-shot super-resolution) 예측이 가능하며, 자료가 부족한 환경에서도 우수한 성능을 보인다.

본 연구에서 다룬 PINNs와 OL 기술은 물리 기반 계산 및 예측 모델링에서 매우 강력한 도구로 자리 잡고 있다. 그러나 이들 기술이 실제 응용과 산업적 활용에서 폭넓게 채택되기 위해서는 몇 가지 한계와 도전 과제를 해결할 필요가 있다. 첫째, 계산 효율성의 문제가 있다. PINNs는 물리적 제약 조건을 손실 함수에 통합함으로써 높은 정확도를 제공하지만, 복잡한 물리 시스템에서는 학습 과정에서 매우 높은 계산 비용이 소요된다. 이를 해결하기 위해 병렬 처리 및 고성능 컴퓨팅 기술의 활용이 필요하며, 효율적인 학습 알고리즘 설계가 요구된다. 반면, OL 기반 기술은 계산 효율성이 상대적으로 높은 편이나, 복잡한 시스템에서는 여전히 상당한 자원이 필요하다. 둘째, 노이즈와 불확실성의 처리는 PINNs와 OL 모두에서 중요한 과제이다. OL 기반 모델은 노이즈에 민감하여 자료 품질이 낮은 경우 성능이 크게 저하될 수 있다. 특히 FNO는 노이즈에 상당히 민감한 신경망이다. 이에 따라 노이즈를 견딜 수 있는 손실 함수 설계와 자료 전처리 기법의 개선이 필요하다. PINNs는 물리적 제약을 통해 노이즈를 완화할 수 있지만, 자료 품질이 지나치게 낮은 경우 성능 한계에 직면할 수 있다. 이러한 문제를 해결하기 위해 Bayesian PINNs와 같은 불확실성을 포함한 접근법에 대한 추가 연구가 필요하다. 셋째, 다중 물리(multiphysics) 및 다중 스케일(multiscale) 문제에 대한 적용성의 확장이 요구된다. 현재 PINNs와 OL은 각각 다중 물리 또는 다중 스케일 문제의 일부 요소에서 효과를 입증했으나, 이들 문제를 종합적으로 해결하기 위해서는 두 기술의 통합 및 최적화가 필요하다. PIDON과 PINO와 같은 초기 하이브리드 모델은 이러한 문제 해결의 가능성을 보여주었으나, 고차원 문제와 다양한 물리적 상호작용을 다룰 수 있는 보다 정교한 프레임워크의 개발이 요구된다. 넷째, 적용 가능한 분야의 확대가 필요하다. 현재 PINNs와 OL은 기상 예측, 유체역학, 재료 과학 등 일부 분야에서 주로 활용되고 있다. 그러나 생물학적 시스템, 에너지 시스템, 재난 관리와 같은 복잡하고 동적인 문제에 대한 적용은 제한적이다. 이들 분야에서 PINNs와 OL을 효과적으로 결합하여 적용할 수 있는 연구가 필요하다. 마지막으로, 정량적 성능 평가를 위한 표준화된 벤치마크의 부족은 이들 기술의 효과적 비교를 어렵게 한다. 따라서 다양한 물리적 문제를 다룰 수 있는 벤치마크 자료셋과 평가 체계를 구축하여, PINNs와 OL 기술의 성능을 객관적으로 검증할 필요가 있다. 이를 통해 기술의 적합성을 판단하고 실제 응용 가능성을 높일 수 있을 것이다.

Acknowledgements

이 논문은 2023학년도 제주대학교 교원성과지원사업에 의하여 연구되었습니다.

References

Amini Niaki S, Haghighat E, Campbell T, Poursartip A, Vaziri R (2021) Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture. Comput Method Appl M 384:113959. doi:10.1016/j.cma.2021.113959

10.1016/j.cma.2021.113959

Baker N, Alexander F, Bremer T, Hagberg A, Kevrekidis Y, Najm H, Parashar M, Patra A, Sethian J, Wild S, Willcox K, Lee S (2019) Workshop report on basic research needs for scientific machine learning: core technologies for artificial intelligence. USDOE Office of Science (SC), Washington DC, 109 p

10.2172/1478744

Bonev B, Kurth T, Hundt C, Pathak J, Baust M, Kashinath K, Anandkumar A (2023) Spherical fourier neural operators: learning stable dynamics on the sphere. In: Proceedings of the 40th International Conference on Machine Learning, ICML 2023, Hawaii, 23-29 July 2023, pp 2806-2823

Cai S, Wang Z, Wang S, Perdikaris P, Karniadakis GE (2021) Physics-informed neural networks for heat transfer problems. J Heat Transf 143(6):060801. doi:10.1115/1.4050542

10.1115/1.4050542

Chen F, Chen F, Sondak D, Protopapas P, Mattheakis M, Liu S, Agarwal D, Di Giovanni M (2020) NeuroDiffEq: a python package for solving differential equations with neural networks. J Open Source Softw 5:1931. doi:10.21105/joss.01931

10.21105/joss.01931

Chen T, Chen H (1995) Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans Neural Netw Learn Syst 6(4):911-917

10.1109/72.39225318263379

Cheng C, Zhang GT (2021) Deep learning method based on physics informed neural network with Resnet block for solving fluid flow problems. Water 13(4):423. doi:10.3390/w13040423

10.3390/w13040423

Choi BJ, Jin HS, Lkhagvasuren B (2024) Applications of the Fourier neural operator in a regional ocean modeling and prediction. Front Mar Sci 11:1383997. doi:10.3389/fmars.2024.1383997

10.3389/fmars.2024.1383997

Cuomo S, Di Cola VS, Giampaolo F, Rozza G, Raissi M, Piccialli F (2022) Scientific machine learning through physics-informed neural networks: Where we are and what's next. J Sci Comput 92(3):88. doi:10.1007/s10915-022-01939-z

10.1007/s10915-022-01939-z

Cybenko G (1989) Approximation by superpositions of a sigmoidal function. Math Control Signals Syst 2(4):303-314

10.1007/BF02551274

Dwivedi V, Srinivasan B (2020) Physics Informed Extreme Learning Machine (PIELM) - a rapid method for the numerical solution of partial differential equations. Neurocomputing 391:96-118. doi:10.1016/j.neucom.2019.12.099

10.1016/j.neucom.2019.12.099

Fang Z (2021) A high-efficient hybrid physics-informed neural networks based on convolutional neural network. IEEE Trans Neural Netw Learn Syst 33(10):5514-5526. doi:10.1109/TNNLS.2021.3070878

10.1109/TNNLS.2021.307087833848251

Gao H, Sun L, Wang JX (2021) PhyGeoNet: physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. J Comput Phys 428:110079. doi:10.1016/j.jcp.2020.110079

10.1016/j.jcp.2020.110079

Gardner JR, Pleiss G, Bindel D, Weinberger KQ, Wilson AG (2018) Gpytorch: blackbox matrix-matrix Gaussian process inference with GPU acceleration. Adv Neural Inf Process Syst 31:7587-7597

Geneva N, Zabaras N (2020) Modeling the dynamics of pde systems with physics-constrained deep auto-regressive networks. J Comput Phys 403:109056. doi:10.1016/j.jcp.2019.109056

10.1016/j.jcp.2019.109056

Guo S (2023) Operator learning via physics-informed DeepONet: Let's implement it from scratch. blog post. https://towardsdatascience.com/operator-learning-via-physics-informed-deeponet-lets-implement-it-from-scratch-6659f3179887 Accessed 1 Dec 2024

Haghighat E, Juanes R (2021) SciANN: A Keras/TensorFlow wrapper for scientific computations and physics-informed deep learning using artificial neural networks. Comput Methods Appl Mech Eng 373:113552. doi:10.48550/arXiv.2005.08803

10.1016/j.cma.2020.113552

He Q, Barajas-Solano D, Tartakovsky G, Tartakovsky AM (2020) Physics-informed neural networks for multiphysics data assimilation with application to subsurface transport. Adv Water Resour 141:103610. doi:10.1016/j.advwatres.2020.103610

10.1016/j.advwatres.2020.103610

Hennigh O, Narasimhan S, Nabian MA, Subramaniam A, Tangsali K, Rietmann M, Ferrandis JdA, Byeon W, Fang Z, Choudhry S (2020) NVIDIA SimNet: an AI-accelerated multi-physics simulation framework. Preprint at arXiv:2012.07938. doi:10.48550/arXiv.2012.07938

10.1007/978-3-030-77977-1_36

Islam M, Thakur MSH, Mojumder S, Hasan MN (2021) Extraction of material properties through multi-fidelity deep learning from molecular dynamics simulation. Comput Mater Sci 188:110187. doi:10.1016/j.commatsci.2020.110187

10.1016/j.commatsci.2020.110187

Jin X, Cai S, Li H, Karniadakis GE (2021) NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J Comput Phys 426:109951. doi:10.1016/j.jcp.2020.109951

10.1016/j.jcp.2020.109951

Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L (2021) Physics-informed machine learning. Nat Rev Phys 3(6):422-440

10.1038/s42254-021-00314-5

Koryagin A, Khudorozkov R, Tsimfer S (2019) PyDEns: a Python framework for solving differential equations with neural networks. Preprint at arXiv:1909.11544 doi:10.48550/arXiv.1909.11544

10.3997/2214-4609.202012125

Kovachki N, Li Z, Liu B, Azizzadenesheli K, Bhattacharya K, Stuart A, Anandkumar A (2023) Neural operator: learning maps between function spaces with applications to PDEs. J Mach Learn Res 24(89):1-97

Li Z, Kovachki N, Azizzadenesheli K, Liu B, Bhattacharya K, Stuart A, Anandkumar A (2021) Fourier neural operator for parametric partial differential equations. arXiv preprint arXiv:2010.08895. doi:10.48550/arXiv.2010.08895

Li Z, Zheng H, Kovachki N, Jin D, Chen H, Liu B, Anandkumar A (2023) Physics-informed neural operator for learning partial differential equations. arXiv preprint arXiv:2111.03794. doi:10.1145/3648506

10.1145/3648506

Lu L, Jin P, Pang G, Zhang Z, Karniadakis GE (2021a) Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell 3:218-229. doi:10.1038/s42256-021-00302-5

10.1038/s42256-021-00302-5

Lu L, Meng X, Cai S, Mao Z, Goswami S, Zhang Z, Karniadakis GE (2022) A comprehensive and fair comparison of two neural operators (with practical extensions) based on fair data. Comput Methods Appl Mech Engrg 393:114778

10.1016/j.cma.2022.114778

Lu L, Meng X, Mao Z, Karniadakis GE (2021b) DeepXDE: a deep learning library for solving differential equations. SIAM Rev 63:208-228

10.1137/19M1274067

Mao Z, Jagtap AD, Karniadakis GE (2020) Physics-informed neural networks for high-speed flows. Comput Methods Appl Mech Engrg 360:112789. doi:10.1016/j.cma.2019.112789

10.1016/j.cma.2019.112789

Moseley B (2021) So, what is a physics-informed neural network?. Blog post. https://benmoseley.blog/my-research/so-what-is-a-physics-informed-neural-network/ Accessed 1 Dec 2024

Novak R, Xiao L, Hron J, Lee J, Alemi AA, Sohl-Dickstein J, Schoenholz SS (2019) Neural tangents: fast and easy infinite neural networks in python. arXiv preprint arXiv:1912.02803. doi:doi.org/10.48550/arXiv.1912.02803

Pathak J, Subramanian S, Harrington P, Raja S, Chattopadhyay A, Mardani M, Kurth T, Hall D, Li Z, Azizzadenesheli K, Hassanzadeh P, Kashinath K, Anandkumar A (2022) Fourcastnet: a global data-driven high-resolution weather model using adaptive fourier neural operators. arXiv preprint arXiv:2202.11214. doi:10.48550/arXiv.2202.11214

Rackauckas C, Nie Q (2017) DifferentialEquations.jl - a performant and feature - rich ecosystem for solving differential equations in Julia. J Open Res Softw 5:15. doi:10.5334/jors.151

10.5334/jors.151

Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput phys 378:686-707

10.1016/j.jcp.2018.10.045

Ramabathiran AA, Ramachandran P (2021) SPINN: sparse, Physics-based, and partially Interpretable Neural Networks for PDEs. J Comput Phys 445:110600. doi:10.1016/j.jcp.2021.110600

10.1016/j.jcp.2021.110600

Schiassi E, Furfaro R, Leake C, Florio MD, Johnston H, Mortari D (2021) Extreme theory of functional connections: a fast physics- informed neural network method for solving ordinary and partial differential equations. Neurocomputing 457:334-356. doi:10.1016/j.neucom.2021.06.015

10.1016/j.neucom.2021.06.015

Serrano L, Le Boudec L, Kassaï Koupaï A, Wang TX, Yin Y, Vittaut JN, Gallinari P (2023) Operator learning with neural fields: tackling PDEs on general geometries. Adv Neural Inf Process Syst 36:70581-70611

Tartakovsky AM, Marrero CO, Perdikaris P, Tartakovsky GD, Barajas-Solano D (2020) Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems. Water Resour Res 56(5):e2019WR026731. doi:10.1029/2019WR026731

10.1029/2019WR026731

Viana FAC, Nascimento RG, Dourado A, Yucesan YA (2021) Estimating model inadequacy in ordinary differential equations with physics-informed neural networks. Comput Struct 245:106458. doi:10.1016/j.compstruc.2020.106458

10.1016/j.compstruc.2020.106458

Waheed UB, Haghighat E, Alkhalifah T, Song C, Hao Q (2021) PINNeik: eikonal solution using physics-informed neural networks. Comput Geosci 155:104833. doi:10.1016/j.cageo.2021.104833

10.1016/j.cageo.2021.104833

Wang N, Chang H, Zhang D (2021a) Theory-guided auto-encoder for surrogate construction and inverse modeling. Comput Methods Appl Mech Engrg 385:114037. doi:10.1016/j.cma.2021.114037

10.1016/j.cma.2021.114037

Wang S, Wang H, Perdikaris P (2021b) Learning the solution operator of parametric partial differential equations with physics-informed DeepONets. Science advances 7(40):eabi8605

10.1126/sciadv.abi860534586842PMC8480920

Wilkinson MD, Dumontier M, Aalbersberg IJ, Appleton G, Axton M, Baak A, Blomberg N, Boiten J-W, Santos LBdS, Bourne PE (2016) The FAIR guiding principles for scientific data management and stewardship. Scientific Data 3(1):1-9

10.1038/sdata.2016.1826978244

Xu K, Darve E (2020) ADCME: Learning spatially-varying physical fields using deep neural networks. Preprint at arXiv:2011.11955. doi:10.48550/arXiv.2011.11955

Yang L, Meng X, Karniadakis GE (2021) B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J Comput Phys 425:109913. doi:10.1016/j.jcp.2020.109913

10.1016/j.jcp.2020.109913

Yang L, Zhang D, Karniadakis GE (2020) Physics-informed generative adversarial networks for stochastic differential equations. SIAM J Sci Comput 42(1):A292-A317. doi:10.1137/18M1225409

10.1137/18M1225409

Yucesan YA, Viana FAC (2021) Hybrid physics-informed neural networks for main bearing fatigue prognosis with visual grease inspection. Comput Ind 125:103386. doi:10.1016/j.compind.2020.103386

10.1016/j.compind.2020.103386

Zhang R, Liu Y, Sun H (2020) Physics-informed multi-LSTM networks for metamodeling of nonlinear structures. Comput Methods Appl Mech Engrg 369:113226. doi:10.1016/j.cma.2020.113226

10.1016/j.cma.2020.113226

Zhu Q, Liu Z, Yan J (2021) Machine learning for metal additive manufacturing: predicting temperature and melt pool fluid dynamics using physics-informed neural networks. Comput Mech 67(2):619-635. doi:10.1007/s00466-020-01952-9

10.1007/s00466-020-01952-9

Zhu Y, Zabaras N, Koutsourelakis PS, Perdikaris P (2019) Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J Comput Phys 394:56-81. doi:10.1016/j.jcp.2019.05.024

10.1016/j.jcp.2019.05.024

Ocean and Polar Research ISSN:2234-7313(Online) Ocean and Polar Research

Preview

A New Paradigm of Artificial Neural Network Learning for Atmospheric and Oceanic Predictions: Physics-Informed Neural Networks and Operator Learning

ABSTRACT

MAIN

Fig. 1.

Conceptualization of SciML

Fig. 2.

Proof of the Universal Approximation Theorem (UAT). (a) A randomly generated function and its graph. (b) Shows that the function on the left can be approximated by a neural network with one layer

Fig. 3.

Three scenarios for a physics-informed approach vs. a data-driven approach

(1)

Fig. 4.

Example of a neural network fitting a model to some experimental data.Adapted from Fig. 1 in Moseley (2021)

(2)

(3)

(4)

Fig. 5.

Loss functions used in physics-based neural networks. Adapted from Fig. 5 in Moseley (2021)

Fig. 6.

The loss function of a neural network that incorporates physics information includes a contribution from the PDE loss, which is an effective measure of whether the predicted solution satisfies the governing differential equation

Table 1.

Major software libraries specifically designed for physics-informed machine learning. Adapted from Table 1 in Karniadakis et al. (2021)

Fig. 7.

Papers related to PINNs by year and applied problems. Here, SE, EE, NSE, and HE represent the one-dimensional Schrödinger equation, the Euler equation, the Navier-Stokes equation, and the Heat equation, respectively. Adapted from Fig. 1 in Cuomo et al. (2022)

Table 2.

Fig. 8.

The structure of DeepONet. Adapted from Fig. 7 in Guo (2023)

Fig. 9.

Learning Operator. (a) The full architecture of neural operator, (b) Fourier layers. Adapted from Fig. 2 in Li et al. (2021)

Fig. 10.

Fig. 11.

Physics-informed DeepONet uses DeepONet as the backbone architecture while leveraging the concept of physics-informed learning to train the model. Adapted from Fig. 10. in Guo (2023)

Fig. 12.

PINO trains neural operator with both training data and PDE loss function. Adapted from Fig. 2 in Li et al. (2023)

Acknowledgements

References